题目内容
已知函数f(x)=2sin2x+2
sinxcosx+1,求:
(1)f(x)的最小正周期;
(2)f(x)的单调递增区间.
| 3 |
(1)f(x)的最小正周期;
(2)f(x)的单调递增区间.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)首先,化简函数解析式,然后,求解函数的最小正周期即可;
(2)结合三角函数的图象与性质进行求解即可.
(2)结合三角函数的图象与性质进行求解即可.
解答:
解:(1)∵f(x)=2sin2x+2
sinxcosx+1
=1-cos2x+
sin2x+1
=2sin(2x-
)+2,
∴T=
=π,
∴f(x)的最小正周期π;
(2)∵-
+2kπ≤2x-
≤
+2kπ,(k∈Z),
∴-
+2kπ≤2x≤
+2kπ,
∴-
+kπ≤x≤
+kπ,(k∈Z).
∴f(x)的单调递增区间[-
+kπ,
+kπ],(k∈Z).
| 3 |
=1-cos2x+
| 3 |
=2sin(2x-
| π |
| 6 |
∴T=
| 2π |
| 2 |
∴f(x)的最小正周期π;
(2)∵-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 3 |
| 2π |
| 3 |
∴-
| π |
| 6 |
| π |
| 3 |
∴f(x)的单调递增区间[-
| π |
| 6 |
| π |
| 3 |
点评:本题主要考查二倍角公式,辅助角公式,两角和与差的三角函数等知识,属于综合性题目,难度中等.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.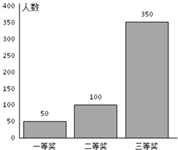 某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.
某超市进行促销活动,规定消费者消费每满100元可抽奖一次.抽奖规则:从装有三种只有颜色不同的球的袋中随机摸出一球,记下颜色后放回,依颜色分为一、二、三等奖,一等奖奖金15元,二等奖奖金10元,三等奖奖金5元.活动以来,中奖结果统计如图所示.消费者甲购买了238元的商品,准备参加抽奖.以频率作为概率,解答下列各题.