题目内容
 如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.
如图,设点P在曲线y=x2,从原点向A(2,4)移动,让直线OP与曲线y=x2所围成图形面积为S1,直线OP、直线x=2与曲线y=x2所围成图形的面积为S2.(1)当S1=S2时,求点P的坐标;
(2)当S1+S2有最小值时,求点P的坐标及此最小值.
考点:抛物线的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)考虑用定积分求两曲线围成的封闭图形面积,再根据S1=S2就可求出t值.
(2)由(1)可求当S1+S2,化简后,为t的三次函数,再利用导数求最小值,以及相应的x值,就可求出P点坐标为多少时,S1+S2有最小值.
(2)由(1)可求当S1+S2,化简后,为t的三次函数,再利用导数求最小值,以及相应的x值,就可求出P点坐标为多少时,S1+S2有最小值.
解答:
解:(1)设点P的横坐标为t(0<t<2),则P点的坐标为(t,t2),
直线OP的方程为y=tx,
S1=
(tx-x2)dx=(
tx2-
x3)
=
t3,S2=
(x2-tx)dx=(
x3-
tx2)
=
-2t+
t3,
因为S1=S2,所以t=
,点P的坐标为(
,
),
(2)S=S1+S2=
t3+
-2t+
t3=
t3-2t+
,
则S′=t2-2,令S′=0得t2-2=0,t=
,
因为0<t<
时,S′<0;
<t<2时,S′>0,
所以,当t=
时,Smin=
,P点的坐标为(
,2).
直线OP的方程为y=tx,
S1=
| ∫ | t 0 |
| 1 |
| 2 |
| 1 |
| 3 |
| | | t 0 |
| 1 |
| 6 |
| ∫ | 2 t |
| 1 |
| 3 |
| 1 |
| 2 |
| | | 2 t |
| 8 |
| 3 |
| 1 |
| 6 |
因为S1=S2,所以t=
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 9 |
(2)S=S1+S2=
| 1 |
| 6 |
| 8 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 8 |
| 3 |
则S′=t2-2,令S′=0得t2-2=0,t=
| 2 |
因为0<t<
| 2 |
| 2 |
所以,当t=
| 2 |
8-4
| ||
| 3 |
| 2 |
点评:本题考查了用定积分求两曲线所围图形面积,以及导数求最值,做题时应认真分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=ln(x+2)在点(-1,0)处的切线方程为( )
| A、x+y+1=0 |
| B、x-y+1=0 |
| C、x-2y+1=0 |
| D、x+2y+1=0 |
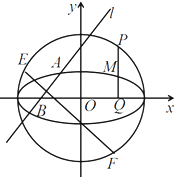 如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.
如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M. 研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:
研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表: