题目内容
在一次对某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组)情况调查中,经统计得到如下2×2列联表:(单位:人)
(Ⅰ)据此判断是否有95%的把握认为参加“篮球小组”或“排球小组”与性别有关?
(Ⅱ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈.已知甲、乙、丙三人都参加“排球小组”.
①求在甲被抽中的条件下,乙丙也都被抽中的概率;
②设乙、丙两人中被抽中的人数为X,求X的分布列及数学期望E(X).
下面临界值表供参考:
参考公式:K2=
.
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
(Ⅱ)在统计结果中,如果不考虑性别因素,按分层抽样的方法从两个兴趣小组中随机抽取7名同学进行座谈.已知甲、乙、丙三人都参加“排球小组”.
①求在甲被抽中的条件下,乙丙也都被抽中的概率;
②设乙、丙两人中被抽中的人数为X,求X的分布列及数学期望E(X).
下面临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:综合题,概率与统计
分析:(Ⅰ)由表中数据得K2的观测值,与临界值比较,即可得出结论;
(Ⅱ)①方法一:令事件A为“甲被抽到”;事件B为“乙丙被抽到”,则P(B|A)=
;方法二:令事件C为“在甲被抽到的条件下,乙丙也被抽到”,则P(C)=
;
②由题知X的可能值为0,1,2,求出相应的概率,可得X的分布列及数学期望E(X).
(Ⅱ)①方法一:令事件A为“甲被抽到”;事件B为“乙丙被抽到”,则P(B|A)=
| P(A∩B) |
| P(A) |
| ||
|
②由题知X的可能值为0,1,2,求出相应的概率,可得X的分布列及数学期望E(X).
解答:
解:(Ⅰ)由表中数据得K2的观测值
k=
=
≈4.582>3.841.…2分
所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.…4分
(Ⅱ)①由题可知在“排球小组”的18位同学中,要选取3位同学.
方法一:令事件A为“甲被抽到”;事件B为“乙丙被抽到”,则
P(A∩B)=
,P(A)=
.
所以P(B|A)=
=
=
=
.…7分
方法二:令事件C为“在甲被抽到的条件下,乙丙也被抽到”,
则P(C)=
=
=
.
②由题知X的可能值为0,1,2.
依题意P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
.
从而X的分布列为
…10分
于是E(X)=0×
+1×
+2×
=
=
.…12分.
k=
| 42×(16×12-8×6)2 |
| 24×18×20×22 |
| 252 |
| 55 |
所以,据此统计有95%的把握认为参加“篮球小组”或“排球小组”与性别有关.…4分
(Ⅱ)①由题可知在“排球小组”的18位同学中,要选取3位同学.
方法一:令事件A为“甲被抽到”;事件B为“乙丙被抽到”,则
P(A∩B)=
| ||
|
| ||
|
所以P(B|A)=
| P(A∩B) |
| P(A) |
| ||
|
| 2 |
| 17×16 |
| 1 |
| 136 |
方法二:令事件C为“在甲被抽到的条件下,乙丙也被抽到”,
则P(C)=
| ||
|
| 2 |
| 17×16 |
| 1 |
| 136 |
②由题知X的可能值为0,1,2.
依题意P(X=0)=
| ||
|
| 35 |
| 51 |
| ||||
|
| 5 |
| 17 |
| ||||
|
| 1 |
| 51 |
从而X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
于是E(X)=0×
| 35 |
| 51 |
| 5 |
| 17 |
| 1 |
| 51 |
| 17 |
| 51 |
| 1 |
| 3 |
点评:考查分类变量的独立性检验,条件概率,随机变量的分布列、数学期望等,中等题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
现要制作一个圆锥形的漏斗,其母线长为l,要使其体积最大,高应为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )
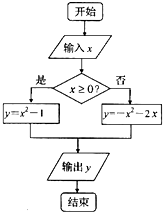

| A、-1或1 | B、-2或0 |
| C、-2或1 | D、-1或0 |
函数y=ln(x+2)在点(-1,0)处的切线方程为( )
| A、x+y+1=0 |
| B、x-y+1=0 |
| C、x-2y+1=0 |
| D、x+2y+1=0 |
已知i为虚数单位,a,b∈R,i(a+i)=b+2i,则a+b等于( )
| A、-1 | B、1 | C、-3 | D、3 |
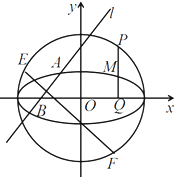 如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.
如图,P是⊙O:x2+y2=4上任意一点,PQ⊥x轴,Q为垂足.设PQ的中点为M.