题目内容
一次考试共有8道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有5道题的答案是正确的,其余题中:有一道题可以判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(Ⅰ)得40分的概率;
(Ⅱ)设所得分数为随机变量X,求X的分布列和数学期望.
(Ⅰ)得40分的概率;
(Ⅱ)设所得分数为随机变量X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(Ⅰ)要得40分,8道选择题必须全做对,在其余三道题中,可以判断两个选项是错误的概率为
,可以判断一个选项是错误的概率为
,可以判断一个选项是错误的概率为
,即可得出结论;
(2)依题意,该考生得分X的取值是25,30,35,40,求出得分X的取每个值的概率,列出分布列,从而求得所得分数的数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(2)依题意,该考生得分X的取值是25,30,35,40,求出得分X的取每个值的概率,列出分布列,从而求得所得分数的数学期望.
解答:
解:(Ⅰ)要得40分,8道选择题必须全做对,在其余三道题中,可以判断两个选项是错误的概率为
,可以判断一个选项是错误的概率为
,可以判断一个选项是错误的概率为
,
所以,得40分的概率为P=
×
×
=
;
(2)依题意,该考生得分X的取值是25,30,35,40,则
P(X=25)=
×
×
=
,
P(X=30)=
×
×
+
×
×
+
×
×
=
,
P(X=35)=
×
×
+
×
×
+
×
×
=
,
P(X=40)=
,
所以X的分布列为:
数学期望EX=25×
+30×
+35×
+40×
=
.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
所以,得40分的概率为P=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 24 |
(2)依题意,该考生得分X的取值是25,30,35,40,则
P(X=25)=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
P(X=30)=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
| 11 |
| 24 |
P(X=35)=
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
P(X=40)=
| 1 |
| 24 |
所以X的分布列为:
| X | 25 | 30 | 35 | 40 | ||||||||
| P |
|
|
|
|
| 1 |
| 4 |
| 11 |
| 24 |
| 1 |
| 4 |
| 1 |
| 24 |
| 365 |
| 12 |
点评:本题考查独立事件的概率,求离散型随机变量的分布列与数学期望,求出离散型随机变量取各个值的概率,是解题的难点.

练习册系列答案
相关题目
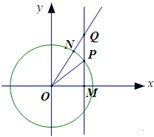 在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<
在直角坐标系xOy中,点p是单位圆上位于第一象限的动点,过p作x轴的垂线与射线y=xtanθ(x≥0,0<θ<