题目内容
已知函数f(x)=ax+
+b.
(1)若f(x)在定义域上单调递增,求实数a的取值范围;
(2)当a=-
时,对任意x∈(0,+∞),b∈(-
,0),xf(x)+c≤0恒成立,求c的取值范围.
| lnx |
| x |
(1)若f(x)在定义域上单调递增,求实数a的取值范围;
(2)当a=-
| 1 |
| 2 |
| 3 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)根据f(x)在定义域上单调递增,在(0,+∞)上f′(x)≥0恒成立可得a≥-
,构造函数g(x)=-
=
,求其最值即可确定a的范围;
(2)把f(x)的解析式代入g(x)=xf(x)+c,由g(x)≤0分离变量c,构造辅助函数后利用导数求辅助函数的最小值,从而求得c的范围.
| 1-lnx |
| x2 |
| 1-lnx |
| x2 |
| lnx-1 |
| x2 |
(2)把f(x)的解析式代入g(x)=xf(x)+c,由g(x)≤0分离变量c,构造辅助函数后利用导数求辅助函数的最小值,从而求得c的范围.
解答:
解:(1)∵f(x)=ax+
+b,
∴f′(x)=a+
,
∵f(x)在定义域上单调递增,
∴在(0,+∞)上f′(x)≥0恒成立,
即a≥-
,
令g(x)=-
=
,则g′(x)=
=
,
当g′(x)>0,即0<x<e
时,f(x)单调递增,
当g′(x)<0,即x>e
时,f(x)单调递减,
∴g(x)max=g(e
)=
.
综上,f(x)在定义域上单调递增时,a≥
.
(2)由g(x)=xf(x)+c=lnx-
x2+bx+c≤0恒成立,
∴c≤
x2-bx-lnx.
记h(x)=
x2-bx-lnx(x>0),则c≤h(x)min.
h′(x)=x-b-
,令h′(x)=0,得x2-bx-1=0.
∴x=
.
当0<x<
时,h′(x)<0,h(x)单调递减,
当x>
时,h′(x)>0,h(x)单调递增,h(x)min=h(
)
令t=
,则t2-bt-1=0,即-bt=1-t2
∴h(
)=
t2+1-t2-lnt=-
t2-lnt+1
令r(t)=-
t2-lnt+1.
∵b∈(-
,0)时,t=
∈(
,1).
又r(t)在(
,1)上单调递减,
∴r(t)>r(1)=
,
∴b∈(-
,0)时,h(x)min>
∴c≤
.
故c的取值范围是(-∞,
].
| lnx |
| x |
∴f′(x)=a+
| 1-lnx |
| x2 |
∵f(x)在定义域上单调递增,
∴在(0,+∞)上f′(x)≥0恒成立,
即a≥-
| 1-lnx |
| x2 |
令g(x)=-
| 1-lnx |
| x2 |
| lnx-1 |
| x2 |
| x-2x(lnx-1) |
| x4 |
| 3-2lnx |
| x3 |
当g′(x)>0,即0<x<e
| 3 |
| 2 |
当g′(x)<0,即x>e
| 3 |
| 2 |
∴g(x)max=g(e
| 3 |
| 2 |
| 1 |
| 2e3 |
综上,f(x)在定义域上单调递增时,a≥
| 1 |
| 2e3 |
(2)由g(x)=xf(x)+c=lnx-
| 1 |
| 2 |
∴c≤
| 1 |
| 2 |
记h(x)=
| 1 |
| 2 |
h′(x)=x-b-
| 1 |
| x |
∴x=
b+
| ||
| 2 |
当0<x<
b+
| ||
| 2 |
当x>
b+
| ||
| 2 |
b+
| ||
| 2 |
令t=
b+
| ||
| 2 |
∴h(
b+
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令r(t)=-
| 1 |
| 2 |
∵b∈(-
| 3 |
| 2 |
b+
| ||
| 2 |
| 1 |
| 2 |
又r(t)在(
| 1 |
| 2 |
∴r(t)>r(1)=
| 1 |
| 2 |
∴b∈(-
| 3 |
| 2 |
| 1 |
| 2 |
∴c≤
| 1 |
| 2 |
故c的取值范围是(-∞,
| 1 |
| 2 |
点评:本题考查了利用导数研究曲线上某点的切线方程,训练了利用导数求函数的最值,体现了数学转化思想方法、分离变量法和函数构造法,解答的关键是对导函数零点的讨论,是高考试卷中的压轴题.

练习册系列答案
相关题目
已知数列{an}是等差数列,a3=-2,前6项的和S6=-3,那么数列{n+an}的前4项的和是( )
| A、-4 | B、-1 | C、5 | D、6 |
若函数f(x)=x3-6ax+5在区间(2,+∞)内是增函数;则实数a的取值范围是( )
| A、a∈(-∞,4] |
| B、a∈(-∞,2] |
| C、a∈[2,+∞) |
| D、a∈[4,+∞) |
执行如图所示的程序框图,则输出结果S的值为( )


A、
| ||
| B、0 | ||
C、-
| ||
| D、-1 |
下列命题中,正确的是( )
| A、若a>b,则ac2>bc2 |
| B、若a+b>a,则b>0 |
| C、若b-a>-a,则b<0 |
| D、若ab>0,则a>0,且b>0 |
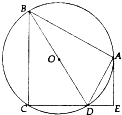 如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.
如图,⊙O是四边形ABCD的外接圆,BD是⊙O的直径,AE⊥CD于点E,∠BDA=∠EDA.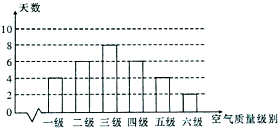 根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表:
根据空气质量指数AQJ(为整数)的不同,可将空气质量分级如下表: