题目内容
4.设集合A={x|x2-2x-3<0},B={x|y=ln(2-x)},则A∩B=( )| A. | {x|-1<x<3} | B. | {x|-1<x<2} | C. | {x|-3<x<2} | D. | {x|1<x<2} |
分析 解不等式求出集合A,求函数定义域得出B,再根据定义写出A∩B.
解答 解:集合A={x|x2-2x-3<0}={x|-1<x<3},
B={x|y=ln(2-x)}={x|2-x>0}={x|x<2},
则A∩B={x|-1<x<2}.
故选:B.
点评 本题考查了集合的化简与运算问题,是基础题.

练习册系列答案
相关题目
15.在等比数列{an}中,已知a3,a7是方程x2-6x+1=0的两根,则a5=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 3 |
12.某几何体的三视图如图所示,若该几何体的体积是12π,则它的表面积是( )
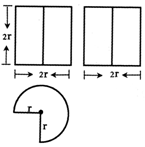

| A. | 18π+16 | B. | 20π+16 | C. | 22π+16 | D. | 24π+16 |
19.设函数f(x)=sin(ωx+φ)(φ>0)的图象关于直线x=-1和x=2对称,则f(0)的取值集合是( )
| A. | {-1,1,-$\frac{1}{2}$} | B. | {1,-$\frac{1}{2}$,$\frac{1}{2}$} | C. | {-1,1,-$\frac{1}{2}$,$\frac{1}{2}$} | D. | {-1,1,-2,2} |
9.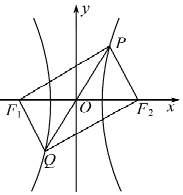 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{5+2\sqrt{5}}$ | D. | $\sqrt{5-2\sqrt{5}}$ |
16.已知$\frac{\overline z}{1+2i}=2+i$,则复数z+5的实部与虚部的和为( )
| A. | 10 | B. | -10 | C. | 0 | D. | -5 |
14.已知集合A={-3,-2,-1},B={x|(x-1)(x+2)≤0,x∈Z},则A∪B=( )
| A. | {-1} | B. | {-2,-1} | C. | {-3,-2,-1,0} | D. | {-3,-2,-1,0,1} |
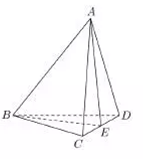 如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;
如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;