题目内容
12.某几何体的三视图如图所示,若该几何体的体积是12π,则它的表面积是( )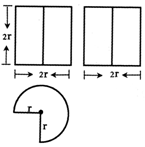
| A. | 18π+16 | B. | 20π+16 | C. | 22π+16 | D. | 24π+16 |
分析 根据三视图可得几何体是圆柱去掉$\frac{1}{4}$个圆柱,圆柱的底面半径为:r;高为:2r,代入体积,求出r,即可求解表面积.
解答 解:由题意可知:几何体是圆柱去掉$\frac{1}{4}$个圆柱,圆柱的底面半径为:r;高为:2r
几何体的体积为:$\frac{3}{4}π{r}^{2}•2r=12π$,∴r=2.
几何体的表面积为:$\frac{3}{4}•2π•2•4+\frac{3}{4}π•{2}^{2}•2+2•2•4$=18π+16.
故选A.
点评 本题考查了由三视图求几何体的表面积与体积,解答此类问题的关键是判断几何体的形状及数据所对应的几何量.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
7.(2-i)(-2+i)=( )
| A. | -5 | B. | -3+4i | C. | -3 | D. | -5+4i |
17.已知集合A={x|x≥3或x≤1},B={x|x2-6x+8<0},则(∁RA)∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
4.设集合A={x|x2-2x-3<0},B={x|y=ln(2-x)},则A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x<2} | C. | {x|-3<x<2} | D. | {x|1<x<2} |