题目内容
9.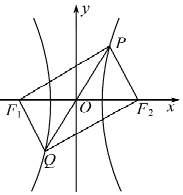 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{5+2\sqrt{5}}$ | D. | $\sqrt{5-2\sqrt{5}}$ |
分析 由题意,矩形的对角线长相等,由此建立方程,找出a,c的关系,即可求出双曲线的离心率.
解答 解:由题意,矩形的对角线长相等,
y=2x代入$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0),可得x=±$\sqrt{\frac{{a}^{2}{b}^{2}}{{b}^{2}-4{a}^{2}}}$,y=±2$\sqrt{\frac{{a}^{2}{b}^{2}}{{b}^{2}-4{a}^{2}}}$,
∴$\frac{5{a}^{2}{b}^{2}}{{b}^{2}-4{a}^{2}}$=c2,
∴5a2b2=(b2-4a2)c2,
∴5a2(c2-a2)=(c2-5a2)c2,
∴e4-10e2+5=0,
∵e>1,∴e2=5+2$\sqrt{5}$,
∴e=$\sqrt{5+2\sqrt{5}}$.
故选:C.
点评 本题考查双曲线的离心率,考查矩形的性质,确定a,c的关系是关键,属于中档题.

练习册系列答案
相关题目
17.已知集合A={x|x≥3或x≤1},B={x|x2-6x+8<0},则(∁RA)∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
4.设集合A={x|x2-2x-3<0},B={x|y=ln(2-x)},则A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x<2} | C. | {x|-3<x<2} | D. | {x|1<x<2} |
19.(x2-x+y)5的展开式中,x4y3的系数为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
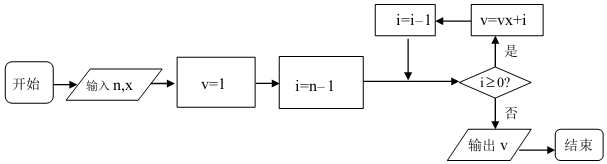
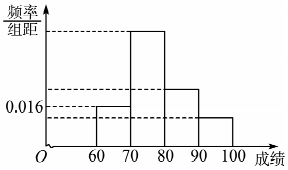 某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.
某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.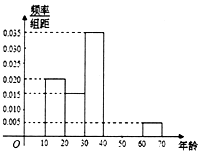 2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.
2017年由央视举办的一档文化益智节目《中国诗词大会》深受观众喜爱,某记者调查了部分年龄在[10,70]的观众,得到如下频率分布直方图.若第四、五、六组的人数依次成等差数列,且第六组有4人.