题目内容
已知定义在R上f（x）的导函数是f′（x）且f′（x）＞1，若a∈R，则f（a+1）-f（a）的一个可能值是（ ）
| A、0 | ||
B、
| ||
| C、1 | ||
| D、2 |
考点：函数的单调性与导数的关系
专题：导数的概念及应用
分析：构造函数g（x）=f（x）-x，利用函数的单调性和导数之间的关系即可得到结论．
解答：
解：设g（x）=f（x）-x，则g′（x）=f′（x）-1＞0，即函数g（x）单调递增，
即g（a+1）＞g（a），
则f（a+1）-（a+1）＞f（a）-a，
即f（a+1）-f（a）＞1，
则满足条件的值为2，
故选：D．
即g（a+1）＞g（a），
则f（a+1）-（a+1）＞f（a）-a，
即f（a+1）-f（a）＞1，
则满足条件的值为2，
故选：D．
点评：本题主要考查函数值的计算，构造函数，利用函数单调性和导数之间的关系是解决本题的关键．
练习册系列答案
相关题目
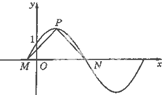如图，函数y=2sin（πx+φ），x∈R（其中0≤φ≤| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
等差数列{an}，{bn}的前n项和分别为Sn，Tn，若
=
，则an=bn时n=（ ）
| Sn |
| Tn |
| 2n+4 |
| 3n+1 |
| A、无解 | B、6 | C、2 | D、无数多个 |
抛物线y2=8x与双曲线
-
=1的一个焦点重合，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
已知双曲线
-
=1(b＞a＞0)的两条渐近线为l1，l2，过右焦点F作垂直l1的直线交l1，l2于A，B两点．若|OA|，|AB|，|OB|成等差数列，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下面几种推理过程是演绎推理的是（ ）
| A、由6=3+3，8=3+5，10=3+7，12=5+7，14=7+7，…，得出结论：一个偶数（大于4）可以写成两个素数的和． | ||||
| B、两条直线平行，两同旁内角互补，因为∠A和∠B是两条平行直线的同旁内角，所以∠A+∠B=180° | ||||
| C、我国地质学家李四光发现中国松辽地区和中亚细亚的地质结构类似，而中亚细亚有丰富的石油，由此，他推断松辽平原也蕴藏着丰富的石油 | ||||
D、在数列{an}中，a1=1，an=
|
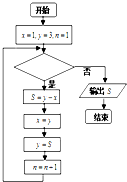已知数列{an}满足a1=1，a2=3，an+2=an+1-an，n∈N*，利用如图所示的程序框图计算该数列的第n项（n≥3），若输出S的结果为1，则判断框内的条件可能是（ ）| A、n≤5？ | B、n≤6？ |
| C、n≤7？ | D、n≤8？ |
下面几个推理过程是演绎推理的是（ ）
| A、某同学第一次数学考试65分，第二次考试68分，由此预测其第三次考试71分 | ||
| B、根据圆的面积为S=πr2，推测球的体积为V=πr3 | ||
C、在数列{an}中，根据a1=1，an+1=
| ||
| D、因为平行四边形的对角线互相平分，而菱形是平行四边形，所以菱形的对角线互相平分 |