题目内容

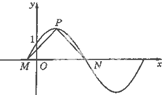如图，函数y=2sin（πx+φ），x∈R（其中0≤φ≤
π
2
）的图象与y轴交于点（0，1）．设P是图象上的最高点，M、N是图象与x轴的交点，则PM与PN的夹角的余弦值为（　　）
A、
3
5
B、-
3
5
C、
15
17
D、-
15
17
考点：正弦函数的图象
专题：三角函数的求值
分析：根据三角函数的图象和性质，求出相应的长度，利用余弦函数的倍角公式，即可得到结论．
解答： 解：当x=0时y=1，即2sinφ=1，即sinφ=
1
2
，
函数的周期T=
2π
π
=2，
则MN=1，AP=2，
则MP=
22+(
1
2
)2
=
17
4
=
17
2
，
则sin∠APM=
AM
MP
=
1
17
，
则cos∠MPN=1-2sin2∠APM=1-2×
1
17
=
15
17
，
故选：C．
点评：本题主要考题三角函数值的计算，根据余弦函数的倍角公式是解决本题的关键．
练习册系列答案
相关题目
平行六面体ABCD-A1B1C1D1的所有棱长均为2，∠A1AD=∠A1AB=∠DAB=60°，那么二面角A1-AD-B的余弦值为
 
．
已知定义域为R的函数f（x）=
b-2x
2x+a
是奇函数．
（1）求a，b的值；
（2）用定义域证明f（x）在（-∞，+∞）上为减函数；
（3）若对于t∈R，不等式f（t2-2t）+f（2t2-k）＜0恒成立，求k的范围．
已知△ABC的三条边的边长分别为4米、5米、6米，将三边都截掉x米后，剩余的部分组成一个钝角三角形，则x的取值范围是（　　）
A、0＜x＜5
B、1＜x＜5
C、1＜x＜3
D、1＜x＜4
已知函数f（x）=log2（
1+25x2
-5x）+3，则f（lna）+f（ln
1
a
）的值（　　）
A、为-6B、为6
C、为0D、与a的取值有关
f（x）=2sinπx-x+1的零点个数为（　　）
A、4B、5C、6D、7
数列{an}满足：a1=
1
3
，且对于任意的正整数m，n都有am+n=am•an，则an=（　　）
A、(
1
3
)n-1
B、
2
3
(
1
3
)n-1
C、(
1
3
)n
D、
1
2
[1-(
1
3
)n]
若f（x）在[a，b]上连续，在（a，b）内可导，且x∈（a，b）时，f′（x）＞0，又f（a）＜0，则（　　）
A、f（x）在[a，b]上单调递增，且f（b）＞0
B、f（x）在[a，b]上单调递增，且f（b）＜0
C、f（x）在[a，b]上单调递减，且f（b）＜0
D、f（x）在[a，b]上单调递增，但f（b）的符号无法判断
已知定义在R上f（x）的导函数是f′（x）且f′（x）＞1，若a∈R，则f（a+1）-f（a）的一个可能值是（　　）
A、0
B、
1
2
C、1
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网