题目内容
20．函数f（x）=-x3+3x2+9x+a，x∈[-2，2]的最小值为-2，则f（x）的最大值为（ ）| A． | 25 | B． | 23 | C． | 21 | D． | 20 |
分析 先将f（x）的各极值与其端点的函数值比较，其中最大的一个就是最大值，最小的一个就是最小值，再根据条件求出a的值，最小值即可求得．
解答 解：求导函数可得f′（x）=-3x2+6x+9=-3（x+1）（x-3）
令f′（x）=-3x2+6x+9=0，解得x=-1或3
∵x∈[-2，-1）时，f′（x）＜0，函数单调减，x∈（-1，2]时，f′（x）＞0，函数单调增，
∴函数在x=-1时，取得最小值，在x=-2或x=2时，函数取得最大值，
∵f（-1）=-5+a=-2，
∴a=3，
∴f（-2）=2+a=5，f（2）=22+a=25，函数的最大值为25，
故选：A．
点评 本题考查了利用导数求闭区间上函数的最值，解题的关键是利用导数工具，确定函数的最值，属于中档题．
练习册系列答案
相关题目
20．
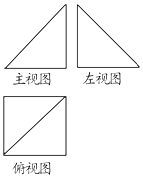如图，已知某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积是（ ）
如图，已知某几何体的主视图和左视图是全等的等腰直角三角形，俯视图是边长为2的正方形，那么它的体积是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 4 | D． | $\frac{16}{3}$ |
11．已知正方形ABCD的边长为2，H是边DA的中点，在正方形ABCD内部随机取一点P，则满足|PH|＜$\sqrt{2}$的概率为（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{π}{8}+\frac{1}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{4}+\frac{1}{4}$ |
8．已知$\overrightarrow{AB}$=（cos23°，cos67°），$\overrightarrow{BC}$=（2cos68°，2cos22°），则△ABC的面积为（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 1 | D． | $\frac{\sqrt{2}}{2}$ |
9．已知点A（-1，1），B（2，-2），若直线l：x+my+m=0与线段AB（含端点）相交，则实数m的取值范围是（ ）
| A． | （-∞，$\frac{1}{2}$]∪[2，+∞） | B． | [$\frac{1}{2}$，2] | C． | （-∞，-2]∪[-$\frac{1}{2}$，+∞） | D． | [-$\frac{1}{2}$，-2] |