题目内容
11.已知正方形ABCD的边长为2,H是边DA的中点,在正方形ABCD内部随机取一点P,则满足|PH|<$\sqrt{2}$的概率为( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{8}+\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{4}+\frac{1}{4}$ |
分析 求得正方形的面积,则S(M)=S△DGH+S△AEH+S扇形EGH,根据几何概率概率公式可知:P(M)=$\frac{S(M)}{{S}_{ABCD}}$,即可求得满足|PH|<$\sqrt{2}$的概率.
解答 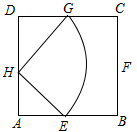 解:(1)如图所示,正方形的面积S正方形ABCD=2×2=4.
解:(1)如图所示,正方形的面积S正方形ABCD=2×2=4.
设“满足|PH|>$\sqrt{2}$的正方形内部的点P的集合”为事件M,
则S(M)=S△DGH+S△AEH+S扇形EGH=2×$\frac{1}{2}$×1×1+$\frac{1}{2}$×$\sqrt{2}$×$\frac{π}{2}$×$\sqrt{2}$=1+$\frac{π}{2}$,
∴P(M)=$\frac{1+\frac{π}{2}}{4}$=$\frac{π}{8}$+$\frac{1}{4}$.
故满足|PH|<$\sqrt{2}$的概率为$\frac{π}{8}$+$\frac{1}{4}$.
故选B.
点评 本题考查几何概率概率公式,考查计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若曲线Cl:x2+y2-2x=0与曲线C2:(x-1)(y-mx-m)=0有四个不同的交点,则实数m的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ |
16.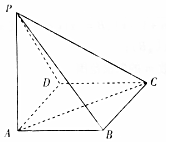 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
 如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )
如图,在底面为正方形的四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
3.在数列{an}中,若存在非零实数T,使得${a_{n+T}}={a_n}({N∈{n^*}})$成立,则称数列{an}是以T为周期的周期数列.若数列{bn}满足bn+1=|bn-bn-1|,且b1=1,b2=a(a≠0),则当数列{bn}的周期最小时,其前2017项的和为( )
| A. | 672 | B. | 673 | C. | 3024 | D. | 1345 |
20.函数f(x)=-x3+3x2+9x+a,x∈[-2,2]的最小值为-2,则f(x)的最大值为( )
| A. | 25 | B. | 23 | C. | 21 | D. | 20 |