题目内容
化简：
．
| cos(-8π-α)+tan(π+α)+cos(α-5π) |
| sin(π-α)+cot(-π-α)+sin(α-5π) |
考点：运用诱导公式化简求值
专题：计算题
分析：运用诱导公式即可化简．
解答：
解：
=
=
=1-sec2α
| cos(-8π-α)+tan(π+α)+cos(α-5π) |
| sin(π-α)+cot(-π-α)+sin(α-5π) |
| cosα+tanα-cosα |
| sinα-cotα-sinα |
| tanα |
| -cotα |
点评：本题主要考查了诱导公式在化简求值时的应用，属于基础题．
练习册系列答案
相关题目
设变量x、y满足
，则目标函数z=2x+3y的最小值为（ ）
|
| A、7 | B、8 | C、22 | D、23 |
等差数列{an}的首项a1=1，公差d=3，{an}的前n项和为Sn，则S10=（ ）
| A、28 | B、31 |
| C、145 | D、160 |
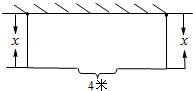如图，某养殖户要建一个面积为800平方米的矩形养殖场，要求养殖场的一边利用旧墙（旧墙的长度大于4米），其他各边用铁丝网围成，且在矩形一边的铁丝网的正中间要留一个4米的进出口．设矩形的宽为x米，铁丝网的总长度为y米．