题目内容
函数f(x)=[x]的函数值表示不超过x的最大整数.
(Ⅰ)求f(1.6)、f(2);
(Ⅱ)记函数g(x)=x-f(x)(0≤x<4),在平面直角坐标系中作出函数g(x)的图象;
(Ⅲ)若方程g(x)-logα﹙x-
﹚=0(α>0且α≠1)有且仅有一个实根,求α的取值范围.
(Ⅰ)求f(1.6)、f(2);
(Ⅱ)记函数g(x)=x-f(x)(0≤x<4),在平面直角坐标系中作出函数g(x)的图象;
(Ⅲ)若方程g(x)-logα﹙x-
| 1 |
| 2 |
考点:函数图象的作法,函数的零点与方程根的关系
专题:函数的性质及应用
分析:(Ⅰ)由函数f(x)=[x],可得f(1.6)和f(2)的值.
(Ⅱ)由 f(x)的解析式求得g(x)=x-f(x)的解析式,从而画出函数g(x)的图象.
(Ⅲ)由题意可得,函数y=g(x)的图象和函数y=logα﹙x-
﹚=0(α>0且α≠1)的图象有且仅有一个交点,当函数y的图象经过点(3,1)时,求得α的值,当函数y的图象经过点(4,1)时,求得α的值,从而得到要求的α的范围.
(Ⅱ)由 f(x)的解析式求得g(x)=x-f(x)的解析式,从而画出函数g(x)的图象.
(Ⅲ)由题意可得,函数y=g(x)的图象和函数y=logα﹙x-
| 1 |
| 2 |
解答:
 解:(Ⅰ)由函数f(x)=[x],可得f(1.6)=[1.6]=1,f(2)=[2]=2.
解:(Ⅰ)由函数f(x)=[x],可得f(1.6)=[1.6]=1,f(2)=[2]=2.
(Ⅱ)∵f(x)=
,(0≤x<4),∴g(x)=x-f(x)=
.
在平面直角坐标系中作出函数g(x)的图象,如图所示:
(Ⅲ)若方程g(x)-logα﹙x-
﹚=0(α>0且α≠1)有且仅有一个实根,
则函数y=g(x)的图象和函数y=logα﹙x-
﹚=0(α>0且α≠1)的图象有且仅有一个交点,
当函数y=logα﹙x-
﹚=0(α>0且α≠1)的图象经过点(3,1)时,α=
;
当函数y=logα﹙x-
﹚=0(α>0且α≠1)的图象经过点(4,1)时,α=
,
故要求的α的范围为(
,
).
 解:(Ⅰ)由函数f(x)=[x],可得f(1.6)=[1.6]=1,f(2)=[2]=2.
解:(Ⅰ)由函数f(x)=[x],可得f(1.6)=[1.6]=1,f(2)=[2]=2.(Ⅱ)∵f(x)=
|
|
在平面直角坐标系中作出函数g(x)的图象,如图所示:
(Ⅲ)若方程g(x)-logα﹙x-
| 1 |
| 2 |
则函数y=g(x)的图象和函数y=logα﹙x-
| 1 |
| 2 |
当函数y=logα﹙x-
| 1 |
| 2 |
| 5 |
| 2 |
当函数y=logα﹙x-
| 1 |
| 2 |
| 7 |
| 2 |
故要求的α的范围为(
| 5 |
| 2 |
| 7 |
| 2 |
点评:本题主要求函数的图象的作法,方程的根的存在性及个数判断,体现了化归与转化、数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
集合M={x|x>0},集合N={x|1-x>0},则M∩N等于( )
| A、(0,1) |
| B、(-∞,0) |
| C、(-∞,-1) |
| D、(-∞,1) |
已知不等式组
表示区域D,过区域D中任意一点P作圆x2+y2=1的两条切线且切点分别为A、B,当∠APB最大时,cos∠APB=( )
|
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
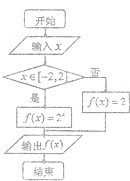 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、(-∞,-2) |
| B、[-2,-1] |
| C、[-1,2] |
| D、(2,+∞) |
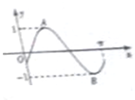 已知函数f(x)=2sinxcos(x-φ)-
已知函数f(x)=2sinxcos(x-φ)-