题目内容
等差数列{an}的首项a1=1,公差d=3,{an}的前n项和为Sn,则S10=( )
| A、28 | B、31 |
| C、145 | D、160 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:把已知数据代入等差数列的求和公式计算可得.
解答:
解:∵等差数列{an}的首项a1=1,公差d=3,
∴S10=10a1+
d=145
故选:C
∴S10=10a1+
| 10×9 |
| 2 |
故选:C
点评:本题考查等差数列的求和公式,属基础题.

练习册系列答案
相关题目
 如图,F1,F2是双曲线C:
如图,F1,F2是双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
集合M={x|x>0},集合N={x|1-x>0},则M∩N等于( )
| A、(0,1) |
| B、(-∞,0) |
| C、(-∞,-1) |
| D、(-∞,1) |
某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.为调查产品的销售情况,现进行两种调查:①从这600个销售点中抽取一个容量为100的样本;②在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,则完成①、②这两项调查宜采用的抽样方法依次是( )
| A、分层抽样法,系统抽样法 |
| B、分层抽样法,简单随机抽样法 |
| C、系统抽样法,分层抽样法 |
| D、简单随机抽样法,分层抽样法 |
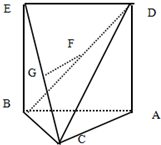 如图5,三角形 A BC中,AC=BC=
如图5,三角形 A BC中,AC=BC=