Question

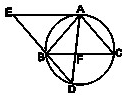（选做题）如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC．过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F．若AB=AC，AE=3

5

，BD=4，则线段CF的长为

 

．

Answer 1

考点：与圆有关的比例线段

专题：直线与圆

分析：由切割线定理得到AE²=EB•ED=EB（EB+BD），求出EB=5，由已知条件推导出四边形AEBC是平行四边形，从而得到AC=AB=BE=5，BC=AE=3

5

，由△AFC∽△DFB，能求出CF的长．

解答： 解：∵AB=AC，AE=3

5

，BD=4，
梯形ABCD中，AC∥BD，BD=4，
由切割线定理可知：AE²=EB•ED=EB（EB+BD），
即45=BE（BE+4），解得EB=5，
∵AC∥BD，∴AC∥BE，
∵过点A作圆的切线与DB的延长线交于点E，
∴∠BAE=∠C，
∵AB=AC，∴∠ABC=∠C，
∴∠ABC=∠BAE，∴AE∥BC，
∴四边形AEBC是平行四边形，
∴EB=AC，∴AC=AB=BE=5，
∴BC=AE=3

5

，
∵△AFC∽△DFB，∴

AC

BD

=

CF

FB

，即

5

4

=

CF

3 5 -CF

，
解得CF=

5 5

3

 ．
故答案为：

5 5

3

．

点评：本题考查与圆有关的线段长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．