题目内容
已知椭圆C:
+y2=1的两个焦点是F1(-c,0),F2(c,0)(c>0).
(Ⅰ)若直线y=x+2与椭圆C有公共点,求m的取值范围;
(Ⅱ)设E是(I)中直线与椭圆的一个公共点,求|EF1|+|EF2|取得最小值时,椭圆的方程;
(Ⅲ)已知斜率为k(k≠0)的直线l与(Ⅱ)中椭圆交于不同的两点A,B,点Q满足
=
且
•
=0,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
| x2 |
| m+1 |
(Ⅰ)若直线y=x+2与椭圆C有公共点,求m的取值范围;
(Ⅱ)设E是(I)中直线与椭圆的一个公共点,求|EF1|+|EF2|取得最小值时,椭圆的方程;
(Ⅲ)已知斜率为k(k≠0)的直线l与(Ⅱ)中椭圆交于不同的两点A,B,点Q满足
| AQ |
| QB |
| NQ |
| AB |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由题意,m+1>1,即m>0,直线y=x+2代入椭圆,利用判别式大于0,即可求m的取值范围;
(Ⅱ)由椭圆的定义可知|EF1|+|EF2|=2
,结合m≥2,即可求出椭圆的方程;
(Ⅲ)设直线l的方程为y=kx+t.代入椭圆方程,消去y得(1+3k2)x2+6ktx+3t2-3=0.由△>0,知t2<1+3k2,设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
,再结合
=
且
•
=0,即可求出截距t的取值范围.
(Ⅱ)由椭圆的定义可知|EF1|+|EF2|=2
| m+1 |
(Ⅲ)设直线l的方程为y=kx+t.代入椭圆方程,消去y得(1+3k2)x2+6ktx+3t2-3=0.由△>0,知t2<1+3k2,设A(x1,y1),B(x2,y2),则x1+x2=-
| 6kt |
| 1+3k2 |
| 3k2-3 |
| 1+3k2 |
| AQ |
| QB |
| NQ |
| AB |
解答:
解:(Ⅰ)由题意,m+1>1,即m>0,
直线y=x+2代入椭圆C:
+y2=1,可得(m+2)x2+4(m+1)x+3(m+1)=0,
△=16(m+1)2-12(m+2)(m+1)=4(m+1)(m-2)≥0,
∴m≥2;
(Ⅱ)由椭圆的定义可知|EF1|+|EF2|=2
,
∵m≥2,
∴m=2时,|EF1|+|EF2|的最小值为2
,
此时椭圆的方程
+y2=1;
(Ⅲ)设直线l的方程为y=kx+t.
代入椭圆方程,消去y得(1+3k2)x2+6ktx+3t2-3=0.
∵直线l与椭圆交于不同两点A、B,
∴△=(6kt)2-4(1+3k2)(3t2-3)>0,
即t2<1+3k2①
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
.
由
=
,得Q为线段AB的中点,
∴xQ=
=-
,yQ=
.
∵
•
=0,
∴kAB•kQN=-1,即
•k=-1.
化简得1+3k2=2t,代入①得t2<2t,解得0<t<2.
又由2t=1+3k2>1,∴t>
.
∴直线l在y轴上的截距t的取值范围是(
,2).
直线y=x+2代入椭圆C:
| x2 |
| m+1 |
△=16(m+1)2-12(m+2)(m+1)=4(m+1)(m-2)≥0,
∴m≥2;
(Ⅱ)由椭圆的定义可知|EF1|+|EF2|=2
| m+1 |
∵m≥2,
∴m=2时,|EF1|+|EF2|的最小值为2
| 3 |
此时椭圆的方程
| x2 |
| 3 |
(Ⅲ)设直线l的方程为y=kx+t.
代入椭圆方程,消去y得(1+3k2)x2+6ktx+3t2-3=0.
∵直线l与椭圆交于不同两点A、B,
∴△=(6kt)2-4(1+3k2)(3t2-3)>0,
即t2<1+3k2①
设A(x1,y1),B(x2,y2),则x1+x2=-
| 6kt |
| 1+3k2 |
| 3k2-3 |
| 1+3k2 |
由
| AQ |
| QB |
∴xQ=
| x1+x2 |
| 2 |
| 3kt |
| 1+3k2 |
| t |
| 1+3k2 |
∵
| NQ |
| AB |
∴kAB•kQN=-1,即
| ||
-
|
化简得1+3k2=2t,代入①得t2<2t,解得0<t<2.
又由2t=1+3k2>1,∴t>
| 1 |
| 2 |
∴直线l在y轴上的截距t的取值范围是(
| 1 |
| 2 |
点评:本题考查椭圆方程的求法和截距t的取值范围.解题时要认真审题,利用椭圆性质注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,过抛物线y2=2px(p>0)的焦点F的两条互相垂直的直线与抛物线分别交于点A、B和C、D;抛物线上的点T(2,t)(t>0)到焦点的距离为3.
如图,过抛物线y2=2px(p>0)的焦点F的两条互相垂直的直线与抛物线分别交于点A、B和C、D;抛物线上的点T(2,t)(t>0)到焦点的距离为3.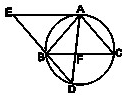 (选做题)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3
(选做题)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3