题目内容
已知椭圆G:
+
=1(a>b>0)的离心率为
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆相交于B,C两点.判断直线MB,MC是否关于直线m对称,并说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆相交于B,C两点.判断直线MB,MC是否关于直线m对称,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出c=1,
=
,由此能求出椭圆的方程.
(Ⅱ)由已知条件得A(-2,0),M(1,
),设直线l:y=
x+n,n≠1.设B(x1,y1),C(x2,y2),由
,得x2+nx+n2-3=0.再由根的判别式和韦达定理结合已知条件能求出直线MB,MC关于直线m对称.
| c |
| a |
| 1 |
| 2 |
(Ⅱ)由已知条件得A(-2,0),M(1,
| 3 |
| 2 |
| 1 |
| 2 |
|
解答:
解:(Ⅰ)∵椭圆G:
+
=1(a>b>0)的离心率为
,
过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限),
∴c=1,(1分)
=
,解得a=2,(2分)
∴b2=a2-c2=3,(3分)
∴椭圆的方程为
+
=1.(4分)
(Ⅱ)∵A为椭圆G的左顶点,∴A(-2,0),M(1,
),(6分)
∴由题意可设直线l:y=
x+n,n≠1.(7分)
设B(x1,y1),C(x2,y2),
由
,得x2+nx+n2-3=0.
由题意得△=n2-4(n2-3)=12-3n2>0,
即n∈(-2,2)且n≠1.(8分)
x1+x2=-n,x1x2=n2-3.(9分)
∵kMB+kMC=
+
,(10分)
=1-
=0,(13分)
所以直线MB,MC关于直线m对称.(14分)
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限),
∴c=1,(1分)
| c |
| a |
| 1 |
| 2 |
∴b2=a2-c2=3,(3分)
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)∵A为椭圆G的左顶点,∴A(-2,0),M(1,
| 3 |
| 2 |
∴由题意可设直线l:y=
| 1 |
| 2 |
设B(x1,y1),C(x2,y2),
由
|
由题意得△=n2-4(n2-3)=12-3n2>0,
即n∈(-2,2)且n≠1.(8分)
x1+x2=-n,x1x2=n2-3.(9分)
∵kMB+kMC=
y1-
| ||
| x1-1 |
y2-
| ||
| x2-1 |
|
=1-
| (n-1)(n+2) |
| n2+n-2 |
所以直线MB,MC关于直线m对称.(14分)
点评:本题考查椭圆方程的求法,考查两条直线是否关于已知直线对称的判断,解题时要认真审题,注意根的判别式和韦达定理的合理运用.

练习册系列答案
相关题目
 如图,椭圆
如图,椭圆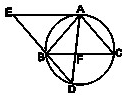 (选做题)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3
(选做题)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3