题目内容

8．用辗转相除法求1813和333的最大公约数时，需要做3次除法．

分析 利用辗转相除法求出1813和333的最大公约数，统计除法的次数可得答案．

解答 解：∵1813=333×5+148，
333=148×2+37，
148=37×4，
故1813和333的最大公约数为37，
在求解过程中共进行了3次除法运算，
故答案为：3．

点评 本题考查了辗转相除法，熟练掌握辗转相除法的运算法则，是解答的关键，本题难度不大，属于基础题

练习册系列答案
相关题目
18．f（x）=x（x-c）2在x=2处有极小值，则常数c的值为（　　）
A．2B．6C．2或6D．1
19．已知$\frac{sinx+1}{cosx}=\frac{1}{2}$，则$\frac{sinx-1}{cosx}$的值是（　　）
A．$\frac{1}{2}$B．2C．$-\frac{1}{2}$D．-2
16．已知函数f（x）=|x-a|-$\frac{1}{2}$x，（a＞0）．
（Ⅰ）若a=3，解关于x的不等式f（x）＜0；
（Ⅱ）若对于任意的实数x，不等式f（x）-f（x+a）＜a2+$\frac{a}{2}$恒成立，求实数a的取值范围．
3．甲、乙两人的各科成绩如茎叶图所示，则下列说法正确的是（　　）
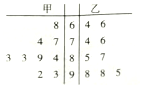
A．甲的中位数是89，乙的中位数是98
B．甲的各科成绩比乙各科成绩稳定
C．甲的众数是89，乙的众数是98
D．甲、乙二人的各科成绩的平均分不相同
13．已知p：-x2+7x+8≥0，q：x2-2x+1-4m2≤0．若“￢p”是“￢q”的充分不必要条件，则实数m的取值范围为[-1，1]．
20．对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（1）给出函数${f_1}（x）=lg\frac{x}{10}，\;\;{f_2}（x）=lg10x，\;\;h（x）=lgx$，h（x）是否为f1（x），f2（x）的生成函数？并说明理由；
（2）设${f_1}（x）={log_2}x，\;\;{f_2}（x）={log_{\frac{1}{2}}}x，\;\;a=2，\;\;b=1$，生成函数h（x）．若不等式3h2（x）+2h（x）+t＞0在x∈[2，4]上恒成立，求实数t的取值范围；
（3）设${f_1}（x）=x\;\;（x＞0），\;\;\;{f_2}（x）=\frac{1}{x}\;\;\;（x＞0）$，取a＞0，b＞0，生成函数h（x）图象的最低点坐标为（2，8）．若对于任意正实数x1，x2且x1+x2=1．试问是否存在最大的常数m，使h（x1）h（x2）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由．
14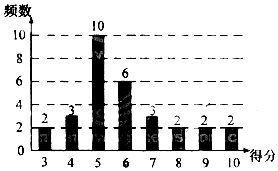．为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为$\overline{x}$，则（　　）
A．m=n=$\overline{x}$B．m=n＜$\overline{x}$C．m＜n＜$\overline{x}$D．n＜m＜$\overline{x}$
15．已知复数z=3-4i（i是虚数单位），则复数$\frac{\overline z}{1+i}$的虚部为（　　）
A．-$\frac{1}{2}$B．$\frac{1}{2}i$C．$\frac{1}{2}$D．$-\frac{1}{2}i$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网