题目内容
7．用数学归纳法证明：（n+1）（n+2）…（n+n）=2n×1×3×…×（2n-1）时，从“k到k+1”左边需增加的代数式是（k+1）（k+2）…（k+k）（4k+1）．分析 从“k到k+1”左边需增加的代数式是：（k+2）（k+3）•…•（k+k）（k+1+k）（k+1+k+1）-（k+1）（k+2）•…•（k+k）．
解答 解：从“k到k+1”左边需增加的代数式是：（k+2）（k+3）•…•（k+k）（k+1+k）（k+1+k+1）-（k+1）（k+2）•…•（k+k）=（k+2）（k+3）•…•（k+k）[（k+1+k）（k+1+k+1）-（k+1）]
=（k+1）（k+2）•…•（k+k）（4k+1），
故答案为：（k+1）（k+2）•…•（k+k）（4k+1）．
点评 本题考查了数学归纳法、作差法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
18．f（x）=x（x-c）2在x=2处有极小值，则常数c的值为（ ）
| A． | 2 | B． | 6 | C． | 2或6 | D． | 1 |
12．向量$\overrightarrow{a}$=（2，4，x），$\overrightarrow{b}$=（2，y，2），若|$\overrightarrow{a}$|=6，且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x+y的值为（ ）
| A． | -3 | B． | 1 | C． | -3或1 | D． | 3或1 |
19．已知$\frac{sinx+1}{cosx}=\frac{1}{2}$，则$\frac{sinx-1}{cosx}$的值是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $-\frac{1}{2}$ | D． | -2 |
14．
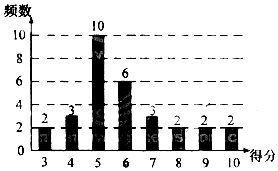为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为$\overline{x}$，则（ ）
为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为m，众数为n，平均值为$\overline{x}$，则（ ）| A． | m=n=$\overline{x}$ | B． | m=n＜$\overline{x}$ | C． | m＜n＜$\overline{x}$ | D． | n＜m＜$\overline{x}$ |