题目内容
9．
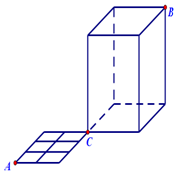如图，一只蚂蚁从点A出发沿着水平面的线条爬行到点C，再由点C沿着置于水平面的长方体的棱爬行至顶点B，则它可以爬行的不同的最短路径有（ ）条．| A． | 40 | B． | 60 | C． | 80 | D． | 120 |
分析 由题意，从A到C最短路径有C53=10条，由点C沿着置于水平面的长方体的棱爬行至顶点B，最短路径有C42=6条，即可求出它可以爬行的不同的最短路径．
解答 解：由题意，从A到C最短路径有C53=10条，由点C沿着置于水平面的长方体的棱爬行至顶点B，最短路径有C42=6条，∴它可以爬行的不同的最短路径有10×6=60条，
故选B．
点评 本题考查最短路径问题，考查组合知识，属于中档题．
练习册系列答案
相关题目
19．若$α∈（0，π），β∈（0，π），\frac{sin2α}{1+cos2α}=\frac{4}{3}，cos（α+β）=\frac{5}{13}$，则sinβ=$\frac{16}{65}$．
20．定义在R上的偶函数f（x）满足f（x）+f（x-1）=0，且在[-5，-4]上是增函数，A，B是锐角三角形的两个内角，则（ ）
| A． | f（sinA）＞f（cosB） | B． | f（sinA）＜f（cosB） | C． | f（sinA）＞f（sinB） | D． | f（cosA）＞f（cosB） |
17．$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
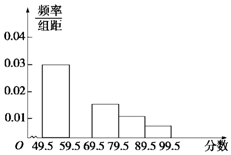在长丰中学举行的电脑知识竞赛中，将九年级两个班参赛的学生成绩（得分均为整数）进行整理后分成五组，绘制如图所示的频率分布直方图．已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30，0.15，0.10，0.05，第二小组的频数是40．
18．f（x）=x（x-c）2在x=2处有极小值，则常数c的值为（ ）
| A． | 2 | B． | 6 | C． | 2或6 | D． | 1 |
19．已知$\frac{sinx+1}{cosx}=\frac{1}{2}$，则$\frac{sinx-1}{cosx}$的值是（ ）
| A． | $\frac{1}{2}$ | B． | 2 | C． | $-\frac{1}{2}$ | D． | -2 |