题目内容
5.设23-2x<23x-4,则x的取值范围是x>$\frac{7}{5}$.分析 利用指数函数的增减性确定出x的范围即可.
解答 解:由y=2x为增函数,且23-2x<23x-4,
得到3-2x<3x-4,
解得:x>$\frac{7}{5}$,
故答案为:x>$\frac{7}{5}$.
点评 此题考查了指、对数不等式的解法,熟练掌握指数函数的性质是解本题的关键.

练习册系列答案
相关题目
16.已知f(x)是定义在区间(0,+∞)上的函数,其导函数为f'(x),且不等式xf'(x)<2f(x)恒成立,则( )
| A. | 4f(1)<f(2) | B. | 4f(1)>f(2) | C. | f(1)<4f(2) | D. | f(1)<2f'(2) |
13.数列{an}中,如果an=49-2n,则Sn取最大值时,n等于( )
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
10.已知函数f(x)是定义在R上的奇函数,且在(0,+∞)上单调递增,若f(-1)=0,则不等式f(2x-1)>0解集为( )
| A. | $({0,\frac{1}{2}})∪({1,+∞})$ | B. | $({-∞,\frac{1}{2}})∪({1,+∞})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})$ |
17.如图为某几何体的三视图,则该几何体的外接球的表面积为( )
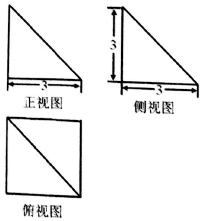

| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |