题目内容
15.设曲线C:y=-lnx(0<x≤1)在M(e-t,t)(t≥0)处的切线为l,若直线l与x轴及y轴所围成的三角形的面积为S(t),则S(t)的最大值是$\frac{2}{e}$.分析 先求导数,可得切线斜率,进而可求切线方程;根据曲线C:y=-lnx(0<x≤1)在点M(e-t,t)(t≥0)处的切线l与x轴y轴所围成的三角形面积为S(t),表示出S(t),再用导数法求解单调区间和最值.
解答 解:∵y=-lnx(0<x≤1)导数f′(x)=-$\frac{1}{x}$,
∴切线l的斜率为-et,
故切线l的方程为y-t=-et(x-e-t),即etx+y-(t+1)=0,
令x=0得y=t+1,又令y=0得x=e-t(t+1),
∴S(t)=$\frac{1}{2}$(1+t)•e-t(t+1)=$\frac{1}{2}$(1+t)2•e-t,
从而S′(t)=$\frac{1}{2}$•e-t(1-t)(1+t).
∵当t∈(0,1)时,S′(t)>0,当t∈(1,+∞)时,S′(t)<0,
∴S(t)的最大值为S(1)=$\frac{2}{e}$,即S(t)的最大值为$\frac{2}{e}$.
故答案为:$\frac{2}{e}$.
点评 本题考查导数的运用:求切线方程和单调区间、极值和最值,考查化简整理的运算能力,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.若$tan({α+\frac{π}{4}})=-3$,则cos2α+2sin2α=( )
| A. | $\frac{9}{5}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | 0 |
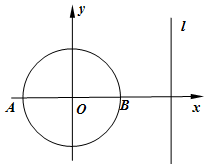 如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.
如图,在平面直角坐标系中,已知圆O:x2+y2=4与直线l:x=4,A,B是圆O与x轴的交点,P是l上的动点.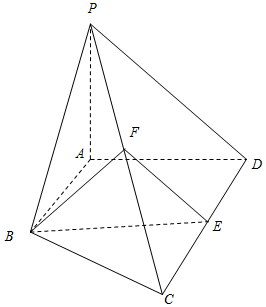 如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.