题目内容
10.(1)计算2cos$\frac{π}{2}$-tan$\frac{π}{4}$+$\frac{3}{4}$tan2$\frac{π}{6}$-sin$\frac{π}{6}$+cos2$\frac{π}{6}$+sin$\frac{3π}{2}$;(2)已知sinx=-$\frac{1}{3}$,求cosx,tanx的值.
分析 (1)利用特殊角的三角函数化简求解即可.
(2)利用同角三角函数基本关系式,化简求解即可.
解答 解:(1)2cos$\frac{π}{2}$-tan$\frac{π}{4}$+$\frac{3}{4}$tan2$\frac{π}{6}$-sin$\frac{π}{6}$+cos2$\frac{π}{6}$+sin$\frac{3π}{2}$
=0-1+$\frac{3}{4}×\frac{1}{3}-\frac{1}{2}+\frac{3}{4}-1$
=-$\frac{3}{2}$;
(2)已知sinx=-$\frac{1}{3}$,则cosx=$±\sqrt{1-si{n}^{2}x}$=$±\frac{2\sqrt{2}}{3}$,
tanx=$\frac{sinx}{cosx}$=±$\frac{\sqrt{2}}{4}$
点评 本题考查诱导公式以及特殊角的三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
1.直线l的参数方程是$\left\{\begin{array}{l}{x=1+2t}\\{y=2-t}\end{array}\right.$(t∈R),则l的斜率为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
5.已知 a1=3,a2=6,且 an+2=an+1-an,则a2011=( )
| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
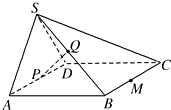 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点. 如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE是等边三角形,AE⊥BE,M为CE上一点,且BM⊥平面ACE.
如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,△BCE是等边三角形,AE⊥BE,M为CE上一点,且BM⊥平面ACE.