题目内容
18.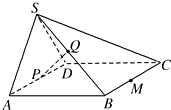 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.(1)求证:PQ∥平面SCD;
(2)求证:;CD⊥SA
(3)若SA=SD,M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?并证明你的结论.
分析 (1)取SC的中点R,连QR,DR.推出PD=$\frac{1}{2}$BC,QR∥BC且QR=$\frac{1}{2}$BC.然后证明四边形PDRQ为平行四边形,即可证明PQ∥平面SCD.
(2)证明CD⊥AD,然后证明CD⊥平面SAD,即可证明结论;
(3)存在点N为SC中点,使得平面DMN⊥平面ABCD.连接PC、DM交于点O,连接PM、SP,证明NO∥SP,NO⊥平面ABCD,然后证明平面DMN⊥平面ABCD.
解答 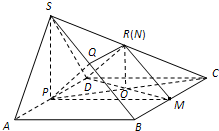 证明:(1)取SC的中点R,连QR,DR.
证明:(1)取SC的中点R,连QR,DR.
由题意知:PD∥BC且PD=$\frac{1}{2}$BC.
在△SBC中,Q为SB的中点,R为SC的中点,
所以QR∥BC且QR=$\frac{1}{2}$BC.
所以QR∥PD且QR=PD,
则四边形PDRQ为平行四边形.
所以PQ∥DR.又PQ?平面SCD,DR?平面SCD,
所以PQ∥平面SCD.…(4分)
(2)因为四边形ABCD为正方形,则CD⊥AD.
又平面SAD⊥平面ABCD,
且面SAD∩面ABCD=AD,
所以CD⊥平面SAD,
所以CD⊥SA.…(8分)
解:(3)N为SC的中点连接PC、DM交于点O,连接PM、SP,
因为PD∥CM,并且PD=CM,
所以四边形PMCD为平行四边形,所以PO=CO.
又因为N为SC中点,
所以NO∥SP.…(12分)
因为平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,并且SP⊥AD,
所以SP⊥平面ABCD,
所以NO⊥平面ABCD,…(13分)
又因为NO?平面DMN,
所以平面DMN⊥平面ABCD.…(14分)
点评 本题考查平面与平面垂直的判定,直线与平面平行的判定,直线与平面垂直的判定,考查空间想象能力.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
9.极坐标方程ρ=2sin($\frac{π}{3}$+θ)化为直角坐标方程为( )
| A. | (x-$\frac{{\sqrt{3}}}{2}$)2+(y-$\frac{1}{2}$)2=1 | B. | y=2(x-$\frac{3}{2}$) | C. | (x-$\frac{{\sqrt{3}}}{2}$)(y-$\frac{1}{2}$)=1 | D. | 4x2+12y2=1 |
6.数列5,9,17,33,x,…中的x等于( )
| A. | 47 | B. | 65 | C. | 63 | D. | 128 |
8.已知两圆x2+y2=10和(x-1)2+(y-3)2=20相交于A,B两点,则公共弦AB的长度等于( )
| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 4 |