题目内容

20．正方体ABCD-A1B1C1D1中，BD1与平面AA1D1D所成的角的正切值是$\frac{\sqrt{2}}{2}$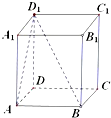

分析 ∠AD1B为BD1与平面AA1D1D所成的角，则tan∠AD1B=$\frac{AB}{A{D}_{1}}$．

解答 解：∵AB⊥平面AA1D1D，
∴∠AD1B为BD1与平面AA1D1D所成的角，
设正方体棱长为1，则AD1=$\sqrt{2}$，
∴tan∠AD1B=$\frac{AB}{A{D}_{1}}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$．
故答案为$\frac{\sqrt{2}}{2}$．

点评 本题考查了正方体的结构特征，线面角的计算，属于中档题．

练习册系列答案
相关题目
10．已知|$\overrightarrow a}$|=3，|$\overrightarrow b}$|=4，且$\overrightarrow a$与$\overrightarrow b$不共线，若（$\overrightarrow a$+k$\overrightarrow b$）⊥（$\overrightarrow a$-k$\overrightarrow b$），则k=$±\frac{3}{4}$．
11．已知△ABC的三边长分别为AB=5，BC=4，AC=3，M是AB边上的点，P是平面ABC外一点，给出下列四个命题：
①若PA⊥平面ABC，则三棱锥P-ABC的四个面都是直角三角形；
②若PM⊥平面ABC，且M是AB边的中点，则有PA=PB=PC；
③若PC=5，PC⊥平面ABC，则△PCM面积的最小值为$\frac{15}{2}$；
④若PC=5，P在平面ABC上的射影是内切圆的圆心O，则PO长为$\sqrt{23}$；
其中正确命题的个数是（　　）
A．1B．2C．3D．4
8．已知函数f（x）=3klnx+$\frac{2{k}^{2}-{x}^{2}}{x}$（k为常数，k＞0）．
（1）当k=1时，求f（x）的极值；
（2）若k∈[3，+∞），曲线y=f（x）上总存在相异两点M（x1，y1），N（x2，y2），使得曲线y=f（x）在M，N两点处的切线互相平行，求x1+x2的取值范围．
15．已知p：（x+2）（x-6）≤0，q：|x-2|＜5，命题“p∨q”为真，“p∧q”为真，求实数x的取值范围．
5．函数f（x）=2x2+2-x+2的图象经过点（1，a），求a的值等于（　　）
A．$\frac{9}{2}$B．$\frac{21}{2}$C．6D．12
12．在下列直线中，与圆x2+y2+4x-2y+4=0相切的直线是（　　）
A．x=0B．y=0C．x+y=0D．x-y=0
9．极坐标方程ρ=2sin（$\frac{π}{3}$+θ）化为直角坐标方程为（　　）
A．（x-$\frac{{\sqrt{3}}}{2}$）2+（y-$\frac{1}{2}$）2=1B．y=2（x-$\frac{3}{2}$）C．（x-$\frac{{\sqrt{3}}}{2}$）（y-$\frac{1}{2}$）=1D．4x2+12y2=1
10．（1）计算2cos$\frac{π}{2}$-tan$\frac{π}{4}$+$\frac{3}{4}$tan2$\frac{π}{6}$-sin$\frac{π}{6}$+cos2$\frac{π}{6}$+sin$\frac{3π}{2}$；
（2）已知sinx=-$\frac{1}{3}$，求cosx，tanx的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网