题目内容
已知定义在R上的函数f(x)满足:①对任意的x,y∈R,都有f(xy)=f(x)+f(y);②当x>1时,f(x)>0
(1)求证:f(1)=0;
(2)求证:对任意的x∈R,都有f(
)=-f(x);
(3)判断f(x)在(-∞,0)上的单调性.
(1)求证:f(1)=0;
(2)求证:对任意的x∈R,都有f(
| 1 |
| x |
(3)判断f(x)在(-∞,0)上的单调性.
考点:抽象函数及其应用,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:(1)令x=y=1,即可求得f(1)=0;
(2)令y=
(x≠0),由f(xy)=f(x)+f(y)及f(1)=0即可证得结论;
(3)任取x1<x2<0,则-x1>-x2>0,作差f(x1)-f(x2)=f(
),易证>f(
)>0,从而可判断f(x)在(-∞,0)上的单调性.
(2)令y=
| 1 |
| x |
(3)任取x1<x2<0,则-x1>-x2>0,作差f(x1)-f(x2)=f(
| x1 |
| x2 |
| x1 |
| x2 |
解答:
解:(1)令x=y=1,则f(1)=2f(1),
∴f(1)=0.
(2)证明:令y=
(x≠0),
则f(x•
)=f(x)+f(
)=f(1)=0,
∴f(
)=-f(x);
(3)任取x1<x2<0,则-x1>-x2>0,
∴
=
>1,
由题意,f(
)>0,
又定义域内任意x、y恒有f(xy)=f(x)+f(y),
∴f(xy)-f(y)=f(x),
∴f(x1)-f(x2)=f(
)>0,
∴f(x1)>f(x2),
∴函数f(x)在(-∞,0)上是减函数.
∴f(1)=0.
(2)证明:令y=
| 1 |
| x |
则f(x•
| 1 |
| x |
| 1 |
| x |
∴f(
| 1 |
| x |
(3)任取x1<x2<0,则-x1>-x2>0,
∴
| -x1 |
| -x2 |
| x1 |
| x2 |
由题意,f(
| x1 |
| x2 |
又定义域内任意x、y恒有f(xy)=f(x)+f(y),
∴f(xy)-f(y)=f(x),
∴f(x1)-f(x2)=f(
| x1 |
| x2 |
∴f(x1)>f(x2),
∴函数f(x)在(-∞,0)上是减函数.
点评:本题考查抽象函数及其应用,着重考查赋值法求值,考查函数单调性的判断与证明,属于中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知函数f(x)为偶函数,若将f(x)的图象向右平移一个单位又得到一个奇函数,若f(2)=-1,则f(1)+f(2)+…+f(2013)等于( )
| A、-1 | B、0 |
| C、-1003 | D、1003 |
已知圆锥的底面半径为R,高为H,则圆锥内接圆柱体的体积最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一几何体的三视图如图所示,圆的半径均为2,则该几何体的 表面积( )
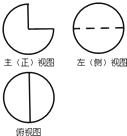

| A、16π | B、14π |
| C、12π | D、8π |
在区间[0,1]上随机取三个数x,y,z,事件A={(x,y,z)|x2+y2+z2<1},则P(A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|