题目内容
求函数f（x）=-x2+x在x=3附近的平均变化率，并求出在该点处的导数．
考点：导数的运算,变化的快慢与变化率
专题：导数的概念及应用
分析：利用平均变化率公式，即可求出函数f（x）=-x2+x在x=3附近的平均变化率和导数
解答：
解：函数f（x）=-x2+x在x=0附近的平均变化率
=
=
=-△x-5．
则f′（3）=
(-△x-5)=-5．
| △y |
| △x |
| f(3+△x)-f(3) |
| △x |
| -(△x)2-5△x |
| △x |
则f′（3）=
| lim |
| △x→0 |
点评：本题考查了平均变化率的意义，考查函数导数的定义和求解，比较基础．
练习册系列答案
相关题目
已知正方形ABCD的边长为4，E，F分别是AB，AD的中点，GC⊥平面ABCD，GC=2，求三棱锥B-EFG的高．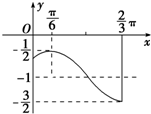
如图，是函数y=Asin（ωx+φ）+k（A＞0，ω＞0）的一段图象．