题目内容
已知函数f（x）=1+a-4asinx-acos2x（a为常数且a≠0，x∈R），求f（x）的最值．
考点：三角函数的最值
专题：三角函数的求值
分析：f（x）=asin2x-4asinx+1，令sinx=t，t∈[-1，1]，则函数即y=at2-4at+1，对称轴为直线x=2．分当a＜0时和a＞0时两种情况，分别利用二次函数的单调性，求得函数y的最值．
解答：
解：f（x）=1+a-4asinx-acos2x=asin2x-4asinx+1，
令sinx=t，t∈[-1，1]，则y=at2-4at+1，对称轴为直线x=2．
a＜0时，y=at2-4at+1在[-1，1]内递增，故当t=-1，ymin=a+4a+1=5a+1；
当t=1，ymax=a-4a+1=-3a+1．
a＞0时，y=at2-4at+1在[-1，1]内递减，故当t=-1，ymax=a+4a+1=5a+1；
当t=1，ymin=a-4a+1=-3a+1．
令sinx=t，t∈[-1，1]，则y=at2-4at+1，对称轴为直线x=2．
a＜0时，y=at2-4at+1在[-1，1]内递增，故当t=-1，ymin=a+4a+1=5a+1；
当t=1，ymax=a-4a+1=-3a+1．
a＞0时，y=at2-4at+1在[-1，1]内递减，故当t=-1，ymax=a+4a+1=5a+1；
当t=1，ymin=a-4a+1=-3a+1．
点评：本题主要正弦函数的定义域和值域，二次函数的性质，体现了转化以及分类讨论的数学思想，属于中档题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
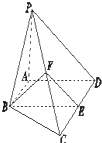（文科）如图，在四棱锥P-ABCD中，平面PAD⊥底面ABCD，PA⊥AD，AB∥CD，AB⊥AD，CD=2AB，E和F分别是CD和PC的中点．求证：