题目内容
已知直线l交椭圆
+
=1于M、N两点，椭圆与y轴的正半轴交于B点，若△MBN的重心恰好落在椭圆的右焦点上，则直线l方程为 ．
| x2 |
| 20 |
| y2 |
| 16 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用重心坐标公式求出弦MN的中点，利用点M（x1，y1），N（x2，y2）在椭圆上，利用点差法，求出斜率，即可求出直线l方程．
解答：
解：设M（x1，y1），N（x2，y2），
又B（0，4），F（2，0），由重心坐标得
=2，
=0
所以弦MN的中点为（3，-2）．
因为点M（x1，y1），N（x2，y2）在椭圆上，所以
，作差得4（x1+x2）（x1-x2）+5（y1+y2）（y1-y2）=0，
将①和②代入得k=
=
，
所以，直线l为：y+2=
（x-3），即6x-5y-28=0．
故答案为：6x-5y-28=0．
又B（0，4），F（2，0），由重心坐标得
| 0+x1+x2 |
| 3 |
| 4+y1+y2 |
| 3 |
所以弦MN的中点为（3，-2）．
因为点M（x1，y1），N（x2，y2）在椭圆上，所以
|
将①和②代入得k=
| y1-y2 |
| x1-x2 |
| 6 |
| 5 |
所以，直线l为：y+2=
| 6 |
| 5 |
故答案为：6x-5y-28=0．
点评：本题考查直线l方程，考查点差法，考查重心坐标公式，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
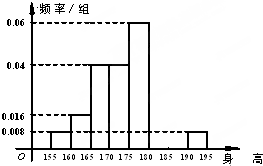从某学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…，第八组[190，195]，右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．先阅读下面的文字：“求
的值时，采用了如下方法：令
=x，则有x=
，两边同时平方，得1+x=x2，解得x=
（负值已舍去）”可用类比的方法，求得1+
的值等于（ ）
1+
|
1+
|
| 1+x |
1+
| ||
| 2 |
| 1 | ||||
2+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
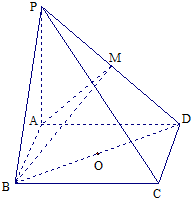如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以BD的中点O为球心、BD为直径的球面交PD于点M．下列说法中正确的是（ ）
| A、一个命题的逆命题为真，则它的逆否命题一定为真 |
| B、“a＞b”与“a+c＞b+c”不等价 |
| C、“a2+b2=0，则a，b全为0”的逆否命题是“若a，b全不为0，则a2+b2≠0” |
| D、一个命题的否命题为真，则它的逆命题一定为真 |