题目内容
已知变量x,y满足约束条件
,则z=2x+3y的取值范围是 .
|
考点:简单线性规划
专题:数形结合
分析:由约束条件作出可行域,化目标函数为直线方程斜截式,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答:
解:由约束条件作可行域如图.

由z=2x+3y,得y=-
x+
,
由图可知,当直线分别经过可行域内的点A(-1,-2)和C(-1,2)时,
目标函数取得最小值和最大值,分别为zmin=2×(-1)+3×(-2)=-8,zmax=2×(-1)+3×2=4.
故答案为:[-8,4].

由z=2x+3y,得y=-
| 2 |
| 3 |
| z |
| 3 |
由图可知,当直线分别经过可行域内的点A(-1,-2)和C(-1,2)时,
目标函数取得最小值和最大值,分别为zmin=2×(-1)+3×(-2)=-8,zmax=2×(-1)+3×2=4.
故答案为:[-8,4].
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则对任意正整数n,下列式子成立的是( )
| f(x2)-f(x1) |
| x2-x1 |
| A、f(n+1)<f(-n)<f(n-1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(-n)<f(n-1)<f(n+1) |
| D、f(n+1)<f(n-1)<f(-n) |
已知函数f(x)=ax2+ax+4(0<a<2),若 x1<x2,x1+x2=1-a,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1)与f(x2)的大小不能确定 |
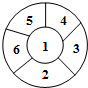 如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有
如图,有一个圆环型花圃,要在花圃的6个部分栽种4种不同颜色的花,每部分栽种1种,且相邻部分栽种不同颜色的花,则不同的栽种方法有