Question

若x，y满足

2x-y-1≥0 x+y-5≥0 y≥1

，则

3x+y-2

x+1

的取值范围是

 

．

Answer 1

考点：简单线性规划的应用

专题：不等式的解法及应用

分析：本题属于线性规划中的延伸题，对于可行域不要求线性目标函数的最值，而是求可行域内的点与点（-1，5）构成的直线的斜率范围．

解答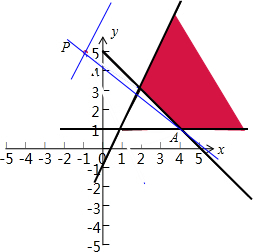： 解：不等式组

2x-y-1≥0 x+y-5≥0 y≥1

表示的区域如图，
z=

3x+y-2

x+1

=3+

y-5

x+1

的几何意义是可行域内的点与点P（-1，5）构成的直线的斜率问题．
当取得点A（4，1）时，

y-5

x+1

=-

4

5

，
当

y-5

x+1

，取y=2x-1的斜率时

y-5

x+1

取得最大值，

11

5

≤3+

y-5

x+1

＜5，
∴

3x+y-2

x+1

的取值范围是：[

11

5

，5)．
故答案为：[

11

5

，5)

点评：本题利用直线斜率的几何意义，求可行域中的点与点（-1，5）的斜率．本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．