题目内容
设A={x|x是锐角},B=(0,1),从集合A到集合B的映射是“求正弦”,则B中元素
相对应的A中的元素是 .
| ||
| 2 |
考点:映射
专题:计算题,函数的性质及应用
分析:由题意,sin60°=
,故B中元素
相对应的A中的元素是60°.
| ||
| 2 |
| ||
| 2 |
解答:
解:由题意,
∵sin60°=
,
则B中元素
相对应的A中的元素是60°.
故答案为:60°.
∵sin60°=
| ||
| 2 |
则B中元素
| ||
| 2 |
故答案为:60°.
点评:本题考查了映射 的定义,属于基础题.

练习册系列答案
相关题目
在△ABC中,
2+
•
<0,则△ABC为( )
| AB |
| AB |
| BC |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角或钝角三角形 |
在△ABC中,若三个内角A,B,C成等差数列且A<B<C,则cosAcosC的取值范围是( )
A、(-
| ||||
B、[-
| ||||
C、(-
| ||||
D、(-
|
已知函数f(x)=sin2x+2
cos2x-
,函数g(x)=mcos(2x-
)-2m+3(m>0),若?x1∈[0,
],总?x2∈[0,
],使得g(x1)=f(x2)成立,则实数m的取值范围为( )
| 3 |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
| A、[1,2] | ||||
B、[1,
| ||||
C、[
| ||||
D、[
|
| 1+2sin(2π-2)cos(2π-2) |
| A、sin2+cos2 |
| B、cos2-sin2 |
| C、-sin2-cos2 |
| D、sin2-cos2 |
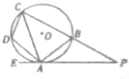 如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明:
如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明: