题目内容
已知函数f（x）=cos2x+2
sinxcosx．
（1）求函数f（x）的最大值，并取得最大值时对应的x的值；
（2）若f（θ）=
，求cos（4θ+
）的值．
| 3 |
（1）求函数f（x）的最大值，并取得最大值时对应的x的值；
（2）若f（θ）=
| 4 |
| 3 |
| π |
| 3 |
考点：三角函数的最值,两角和与差的正弦函数
专题：常规题型,三角函数的图像与性质
分析：（1）先利用两角和的正弦公式化成标准形式，然后根据正弦函数的最值求解函数的最大值；（2）根据f（θ）=
，得sin（2θ+
）的值，然后利用倍角公式求cos（4θ+
）的值．
| 4 |
| 3 |
| π |
| 6 |
| π |
| 3 |
解答：
解：（1）f（x）=cos2x+2
sinxcosx
=2sin（2x+
）
所以f（x）的最大值为2．
当2x+
=2kπ+
，即x=kπ+
，k∈Z时取最大值．
（2）由已知2sin（2θ+
）=
得：sin（2θ+
）=
．
∴cos（4θ+
）=cos2（2θ+
）
=1-2sin2（2θ+
）=
．
| 3 |
=2sin（2x+
| π |
| 6 |
所以f（x）的最大值为2．
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
（2）由已知2sin（2θ+
| π |
| 6 |
| 4 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
∴cos（4θ+
| π |
| 3 |
| π |
| 6 |
=1-2sin2（2θ+
| π |
| 6 |
| 1 |
| 9 |
点评：本题考查了三角函数的图象与性质及三角函数的求值问题，研究三角函数的性质关键是化成标准形式；三角函数求值问题关键是选择适当的公式，根据角的关系建立已知表达式和求解的表达式之间的关系．
练习册系列答案
53天天练系列答案
相关题目
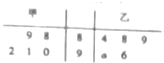某机械厂今年进行了五次技能考核，其中甲、乙两名技术骨干得分的平均分相等，成绩统计情况如茎叶图所示（其中a是0-9的某个整数
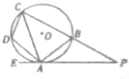如图，四边形ABCD内接于⊙O，过点A作⊙O的切线EP交CB的延长于P，已知∠EAD=∠PCA，证明：在△ABC中，若三个内角A，B，C成等差数列且A＜B＜C，则cosAcosC的取值范围是（ ）
A、(-
| ||||
B、[-
| ||||
C、（-
| ||||
D、（-
|