题目内容
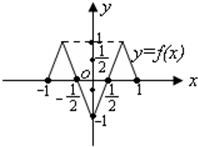 已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是
已知函数y=f(x)的定义域和值域都是[-1,1](其图象如图所示),函数g(x)=sinx,x∈[-π,π].定义:当f(x1)=0(x1∈[-1,1])且g(x2)=x1(x2∈[-π,π])时,称x2是方程f(g(x))=0的一个实数根.则方程f(g(x))=0的所有不同实数根的个数是考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:通过图象可知方程f(x)=0数有4个非零实数解,分别为-1,-
,
,1,分别令g(x)=sinx=-1,-
,
,1,求得对应的x值,从而得出正确结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:当f(x1)=0(x1∈[-1,1])且g(x2)=0,即f[g(x)]=0
通过图象可知方程f(x)=0有4个非零实数解,分别为-1,-
,
,1,
∵函数g(x)=sinx,x∈[-π,π],∴g(x)∈[-1,1].
当g(x)=sinx=-1时,x=-
;当g(x)=sinx=-
时,x=-
,或 x=-
;
当g(x)=sinx=
时,x=
,或x=
;当g(x)=sinx=1时,x=
;
因此,方程f(g(x))=0的所有不同实数根的个数是6个,
故答案为:6.
通过图象可知方程f(x)=0有4个非零实数解,分别为-1,-
| 1 |
| 2 |
| 1 |
| 2 |
∵函数g(x)=sinx,x∈[-π,π],∴g(x)∈[-1,1].
当g(x)=sinx=-1时,x=-
| 3π |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
当g(x)=sinx=
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 2 |
因此,方程f(g(x))=0的所有不同实数根的个数是6个,
故答案为:6.
点评:本题考查根的存在性及根的个数判断,函数的图象,考查逻辑思维能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知奇函数f(x)在(-∞,0)上是单调减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A、{x|-3<x<-1} |
| B、{x|-1<x<1或1<x<3} |
| C、{x|-3<x<0或1<x<3} |
| D、{x|-3<x<1或x>2} |
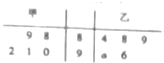 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数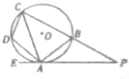 如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明:
如图,四边形ABCD内接于⊙O,过点A作⊙O的切线EP交CB的延长于P,已知∠EAD=∠PCA,证明: