题目内容

若函数f（x）=
k-2x
1+k•2x
（k为常数）在定义域R上为奇函数，则k=
 
．
考点：函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由函数f（x）=
k-2x
1+k•2x
（k为常数）在定义域R上为奇函数可知，f（0）=k=0．
解答： 解：∵函数f（x）=
k-2x
1+k•2x
（k为常数）在定义域R上为奇函数，
∴f（0）=k=0，
故答案为；0．
点评：本题考查了函数的奇偶性的应用，利用特值法求参数，属于基础题．
练习册系列答案
相关题目
函数y=|x2+2x-3|+k的图象与x轴有4个交点，则实数k的取值范围是
 
．
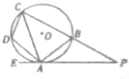如图，四边形ABCD内接于⊙O，过点A作⊙O的切线EP交CB的延长于P，已知∠EAD=∠PCA，证明：
（1）AD=AB；
（2）DA2=DC•BP．
已知函数f（x）=2sin（ωx+
π
6
）（ω＞0），函数f（x）的图象与x轴两个相邻交点的距离为π，则f（x）的单调递增区间是
 
．
求下列函数的导数．
（1）y=（2x2-3）（x2-4）；
（2）y=
x-1
x+1
．
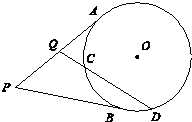如图，p为⊙O外一点，过P点作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=1，CD=4，则PB=
 
．
在△ABC中，
AB
2+
AB
•
BC
＜0，则△ABC为（　　）
A、锐角三角形
B、直角三角形
C、钝角三角形
D、锐角或钝角三角形
在△ABC中，若三个内角A，B，C成等差数列且A＜B＜C，则cosAcosC的取值范围是（　　）
A、(-
1
2
，
1
4
]
B、[-
3
4
，
1
4
]
C、（-
1
2
，
1
4
）
D、（-
3
4
，
1
4
）
已知f（x）=
2
x2+1
，则f（x）的值域为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网