题目内容

点P是以F为焦点的抛物线y2=4x上的动点，则以P为圆心，以线段PF的长为半径的圆与直线x=-1的位置关系是（　　）
A、相切B、相交
C、相离D、随点P的位置变化而变化
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由抛物线的定义，圆心到焦点的距离等于圆心到准线x=-1的距离，所以刚好相切．
解答： 解：F（1，0）为抛物线焦点，圆心在抛物线上，由抛物线的定义，圆心到焦点的距离等于圆心到准线x=-1的距离，所以刚好相切，
故选A．
点评：本题考查直线与圆的位置关系，考查抛物线的定义，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数loga
1-x
x+1
（0＜a＜1）在区间（a，1）上的值域是（1，+∞），则实数a的值为
 
．
2012年伦敦奥运会伦敦站的火炬传递中邀请了5位奥运冠军和3位歌手参加传递，
（Ⅰ） 若3位歌手互不相邻，求伦敦站的不同传递方案的种数．（直接用数字作答）
（Ⅱ）在这8位参加传递的人中选3人参加一项奥运宣传活动，用X表示参加此次宣传活动的歌手的人数．
①列出X的所有可能的取值结果；        
②求随机变量X的分布列；   
③求参加此次活动的人中歌手至少有2名的概率．
函数y=|x2+2x-3|+k的图象与x轴有4个交点，则实数k的取值范围是
 
．
已知函数f（x）=x3-ax2+10，
（I）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）在区间[4，6]内至少存在一个实数x，使得f（x）＜0成立，求实数a的取值范围．
（Ⅲ）当a=1时，设函数g（x）=lnx-2x2+4x+t（t为常数），若使g（x）≤x+m≤f（x）+x-10在（0，+∞）上恒成立的实数m有且只有一个，求实数m和t的值．
2012年欧洲杯足球赛将于6月份在波兰和乌克兰两个国家举行，东道主波兰所在的A组共有四支球队，四支球队之间进行单循环比赛，共进行的比赛的场数为（　　）
A、6B、12C、3D、8
数列{an}的前n项和Sn=n2•an（n≥2），而a1=1，通过计算a2，a3，a4，猜想an=
 
．
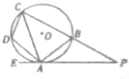如图，四边形ABCD内接于⊙O，过点A作⊙O的切线EP交CB的延长于P，已知∠EAD=∠PCA，证明：
（1）AD=AB；
（2）DA2=DC•BP．
在△ABC中，
AB
2+
AB
•
BC
＜0，则△ABC为（　　）
A、锐角三角形
B、直角三角形
C、钝角三角形
D、锐角或钝角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网