题目内容
7.设等差数列{an}的公差为d,前n项和为Sn,已知a5=9,S7=49.(1)求数列{an}的通项公式;
(2)令bn=an•2n,求数列{bn}的前n项和.
分析 (1)由S7=49结合等差数列的性质求得a4=7,再求等差数列的公差和通项式;
(2)bn=an•2n=(2n-1)•2n,用错位相减法求数列{bn}的前n项和为Tn
解答 解:(1)在等差数列{an}中,由S7=7(a1+a7)=49,得:a4=7,又∵a5=9,∴公差d=2,a1=1,
∴数列{an}的通项公式an=2n-1 (n∈N+),
(2)bn=an•2n=(2n-1)•2n,
令数列{bn}的前n项和为Tn,
Tn=1×21+3×22+5×23+…+(2n-3)×2n-1+(2n-1)•2n…①
2 Tn=1×22+3×23++…+(2n-5)×2n-1+(2n-3)•2n+(2n-1)•2n+1…②
-Tn=2+2(22+23++…+2n-1+•2n)-(2n-1)•2n+1=2+2n+2-8-+(2n-1)•2n+1;
∴Tn=(2n-3)2n+1+6.
点评 本题考查了等差数列的通项,及错位相减法求和,属于基础题.

练习册系列答案
相关题目
17.设集合$A=\left\{{x|\frac{2}{x+1}≥1}\right\}$,集合B={y|y=2x,x<0},则A∪B=( )
| A. | (-1,1] | B. | [-1,1] | C. | (-∞,1] | D. | [-1,+∞) |
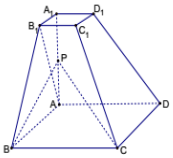 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为AA1的中点.