题目内容
2．设{an}（n∈N*）是各项为正数的等比数列，q是其公比，Tn是其前n项的积，且T5＜T6，T6=T7＞T8，则下列结论错误的是（ ）| A． | 0＜q＜1 | B． | a7=1 | ||
| C． | T6与T7均为Tn的最大值 | D． | T9＞T5 |
分析 由等比数列的单调性和通项公式逐个选项验证可得．
解答 解：∵{an}是各项为正数的等比数列，q是其公比，Tn是其前n项的积，
由T6=T7可得a7=1，故B正确；
由T5＜T6可得a6＞1，∴q=$\frac{{a}_{7}}{{a}_{6}}$∈（0，1），故A正确；
由{an}是各项为正数的等比数列且q∈（0，1）可得数列单调递减，
∴T9＜T5，故D错误；
结合T5＜T6，T6=T7＞T8，可得C正确．
故选：D．
点评 本题考查等比数列的性质，涉及数列的单调性，属中档题．
练习册系列答案
相关题目
12．已知函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$），在同一周期内，$x=\frac{π}{9}$时取得最大值$\frac{1}{2}$，$x=\frac{4}{9}π$时取得最小值-$\frac{1}{2}$，则该函数解析式为（ ）
| A． | $y=2sin（\frac{x}{3}-\frac{π}{6}）$ | B． | $y=\frac{1}{2}sin（3x+\frac{π}{6}）$ | C． | $y=\frac{1}{2}sin（3x-\frac{π}{6}）$ | D． | $y=\frac{1}{2}sin（\frac{x}{3}-\frac{π}{6}）$ |
13．运行如图所示程序，若输出的实数x∈[15，17]，则输入的实数x的取值范围是（ ）
| A． | $[3，\frac{7}{2}]$ | B． | $[1，\frac{5}{4}]$ | C． | [63，71] | D． | [127，143] |
10．已知函数y=$\frac{1}{3}$x3-x+c的图象与x轴恰有两个公共点，则c=（ ）
| A． | $±\frac{2}{3}$ | B． | $\frac{4}{3}$或$\frac{2}{3}$ | C． | -1或1 | D． | $-\frac{4}{3}$或$-\frac{2}{3}$ |
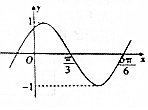已知函数y=sin（ωx+φ）（ω＞0，0＜φ≤$\frac{π}{2}$）的部分图象如图所示，则cos（5ωφ）=-$\frac{1}{2}$．