题目内容
18.若圆C1:x2+y2+2x+2y+1=0与圆C2:x2+y2-4x-6y+m=0外切,则m=-3.分析 化圆的一般方程为标准方程,求出两圆的圆心坐标和半径,由两圆圆心距间的距离与两圆半径的关系列式求得m值.
解答 解:圆C1:x2+y2+2x+2y+1=0化为(x+1)2+(y+1)2=1,圆心坐标为(-1,-1),半径为1;
圆C2:x2+y2-4x-6y+m=0化为(x-2)2+(y-3)2=13-m,圆心坐标为(2,3),半径为$\sqrt{13-m}$.
∵两圆外切,∴$\sqrt{(-1-2)^{2}+(-1-3)^{2}}=1+\sqrt{13-m}$,解得m=-3.
故答案为:-3.
点评 本题考查圆与圆的位置关系,考查两点间距离公式的应用,是基础的计算题.

练习册系列答案
相关题目
8.若三棱锥P-ABC中,AB=AC=1,AB⊥AC,PA⊥平面ABC,且直线PA与平面PBC所成角的正切值为$\frac{1}{2}$,则三棱锥P-ABC的外接球的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
9.将一个总数为A、B、C三层,其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本,则应从C中抽取( )个个体.
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
13.下列判断错误的是( )
| A. | “若m>0,则方程x2+x-m=0有两个不同的实数根”是真命题. | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| C. | 若命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. | |
| D. | 若p∧q为假命题,则p,q均为假命题. |
10.已知数列{an}的前n项和为Sn,且a1=2,an+1=Sn+1(n∈N*),则S5=( )
| A. | 31 | B. | 42 | C. | 37 | D. | 47 |
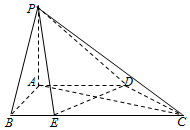 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.