题目内容
6.为了了解参加运动会的2 000名运动员的年龄情况,从中抽取20名运动员的年龄进行统计分析.就这个问题,下列说法中正确的有④⑥.①2 000名运动员是总体;
②每个运动员是个体;
③所抽取的20名运动员是一个样本;
④样本容量为20;
⑤这个抽样方法可采用随机数表法抽样;
⑥每个运动员被抽到的机会相等.
分析 ①②③④⑤⑥利用统计中总体、个体、样本容量的概念及抽样方法、特点等对①②③④⑤⑥六个选项逐一分析即可得到答案.
解答 解:①2000名运动员的年龄是总体,故①错误;
②每个运动员的年龄是个体,故②错误;
③所抽取的20名运动员的年龄是一个样本,故③错误;
④从2000名运动员的年龄中抽取20名运动员的年龄进行统计分析,样本容量为20,正确;
⑤随机数法常常用于总体个数较少时,它的主要特征是从总体中逐个抽取,当总体中的个体数较多时,编号复杂,将总体“搅拌均匀”也比较困难,用随机法产生的样本代表性差的可能性很大,故⑤错误;
⑥每个运动员被抽到的机会相等,正确.
故答案为:④⑥.
点评 本题考查概率统计中的总体、个体、样本容量的概念及抽样方法的判断,准确掌握概念是关键,属于中档题.

练习册系列答案
相关题目
17.若f(x)=sinα-cosx,则f′(x)等于( )
| A. | 2sinα+cosx | B. | cosα+sinx | C. | cosx | D. | sinx |
14.已知两正数x,y 满足x+y=1,则z=$(x+\frac{1}{x})(y+\frac{1}{y})$的最小值为( )
| A. | $\frac{33}{4}$ | B. | $\frac{25}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{17}}}{4}$ |
11.a、b均为实数,则a<b<0是a2>b2的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.已知椭圆:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<3),左右焦点分别为F1,F2,过F1的直线l交椭圆于A、B两点,若|BF2|+|AF2|的最大值为10,则b的值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
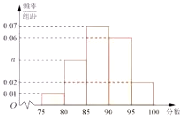 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格: