Question

20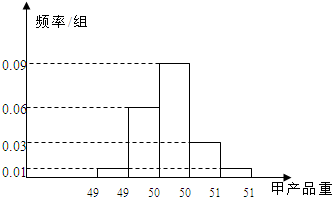．某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本．经统计，得到关于产品重量的样本频率分布直方图和样本频数分布表：

乙流水线 产品重量（单位：克）	频数
（490，495]	6
（495，500]	8
（500，505]	14
（505，510]	8
（510，515]	4

已知产品的重量合格标准为：重量值落在（495，510]内的产品为合格品；否则为不合格品．
（1）从甲流水线样本的合格品中任意取2件，求重量值落在（505，510]的产品件数X的分布列；
（2）从乙流水线中任取2件产品，试根据样本估计总体的思想，求其中合格品的件数Y的数学期望；
（3）从甲、乙流水线中各取2件产品，用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”，并用A表示事件“关于x的一元二次方程2x²+2ξx+ξ=0没有实数解”． 试根据样本估计总体的思想，求事件A的概率．

Answer 1

分析 （1）样本频率分布直方图知，甲样本中合格品数为12+18+6=36，其中重量值落在（505，510]的产品为6件．X的可能取值为0，1，2，利用P（X=k）=$\frac{{∁}_{6}^{k}•{∁}_{30}^{2-k}}{{∁}_{30}^{2}}$（k=0，1，2）．即可得出分布列．
（2）由频数分布表知，乙样本中合格品数为8+14+8=30件，若从乙样本中任取一件产品，该产品为合格品的概率P=$\frac{3}{4}$．根据样本估计总体的思想，可估计从乙流水线上任取一件产品，该产品为合格品的概率$\frac{3}{4}$．从乙流水线上所取的2件产品互不影响，该问题可看成2次独立重复试验，可得合格品的件数Y～B$（2，\frac{3}{4}）$．
（3）由方程2x²+2ξx+ξ=0没有实数解，得△＜0，解得ξ=1．记“从甲流水线中任取2件产品，其中合格品的件数”为Z，“从乙流水线中任取2件产品，其中合格品的件数”为Y，则ξ=|Z-Y|．Z与Y都有0，1，2三种可能的取值，事件A（即ξ=1）包含四种情况：$\left\{\begin{array}{l}{Z=0}\\{Y=1}\end{array}\right.$或$\left\{\begin{array}{l}{Z=1}\\{Y=0}\end{array}\right.$或$\left\{\begin{array}{l}{Z=1}\\{Y=2}\end{array}\right.$或$\left\{\begin{array}{l}{Z=2}\\{Y=1}\end{array}\right.$．进而得出．

解答 解：（1）样本频率分布直方图知，甲样本中合格品数为12+18+6=36，其中重量值落在（505，510]的产品为6件．X的可能取值为0，1，2，
且P（X=k）=$\frac{{∁}_{6}^{k}•{∁}_{30}^{2-k}}{{∁}_{30}^{2}}$（k=0，1，2）．P（X=0）=$\frac{29}{42}$，P（X=1）=$\frac{2}{7}$，P（X=2）=$\frac{1}{42}$．∴X的分布列为：

X	0	1	2
P	$\frac{29}{42}$	$\frac{2}{7}$	$\frac{1}{42}$

（2）由频数分布表知，乙样本中合格品数为8+14+8=30件，
∴若从乙样本中任取一件产品，该产品为合格品的概率P=$\frac{3}{4}$．
根据样本估计总体的思想，可估计从乙流水线上任取一件产品，该产品为合格品的概率P=$\frac{3}{4}$．
∵从乙流水线上所取的2件产品互不影响，该问题可看成2次独立重复试验，
∴合格品的件数Y～B$（2，\frac{3}{4}）$．
∴EY=2×$\frac{3}{4}$=$\frac{3}{2}$，
即合格品的件数Y的数学期望为$\frac{3}{2}$．
（3）由方程2x²+2ξx+ξ=0没有实数解，得△=4ξ²-8ξ＜0，
解得0＜ξ＜2，∴ξ=1．
记“从甲流水线中任取2件产品，其中合格品的件数”为Z，“从乙流水线中任取2件产品，其中合格品的件数”为Y，则ξ=|Z-Y|．
∵Z与Y都有0，1，2三种可能的取值，
∴事件A（即ξ=1）包含四种情况：$\left\{\begin{array}{l}{Z=0}\\{Y=1}\end{array}\right.$或$\left\{\begin{array}{l}{Z=1}\\{Y=0}\end{array}\right.$或$\left\{\begin{array}{l}{Z=1}\\{Y=2}\end{array}\right.$或$\left\{\begin{array}{l}{Z=2}\\{Y=1}\end{array}\right.$．
由（2）知，从乙流水线上任取一件产品，该产品为合格品的概率P=$\frac{3}{4}$．
仿（2）的做法，可知从甲流水线上任取一件产品，该产品为合格品的概率P=$\frac{9}{10}$．
∵从同一条流水线上所取的2件产品互不影响，不同流水线上的取法之间也互不影响，∴P（ξ=1）=$（\frac{1}{10}）^{2}$×${∁}_{2}^{1}×\frac{3}{4}×\frac{1}{4}$+${∁}_{2}^{1}×\frac{9}{10}×\frac{1}{10}×（\frac{1}{4}）^{2}$+${∁}_{2}^{1}×\frac{9}{10}×\frac{1}{10}×（\frac{3}{4}）^{2}$+$（\frac{9}{10}）^{2}$×${∁}_{2}^{1}×\frac{3}{4}$×$\frac{1}{4}$=$\frac{21}{50}$．
所以事件A的概率P（A）=P（ξ=1）=$\frac{21}{50}$．

点评 本题考查了频率分布直方图、二项分布列及其概率计算公式及其数学期望，考查了分类讨论方法、推理能力与计算能力，属于中档题．