题目内容
5.有四个游戏盘,如图所示,(其中A的外形为正方形;B的外形为正六边形;C的外形为正方形;D.的外形为圆,D.的阴影部分为等腰直角三角形)撒一粒黄豆到游戏盘,如果落在阴影部分,则可中奖.你希望中奖机会大,你应当选择的游戏盘为( )| A. |  | B. |  | C. |  | D. | 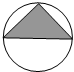 |
分析 先明确是几何概型中的面积类型,分别求三角形与扇形的面积,然后求比值,再比较大小.
解答 解:对于A,游戏盘的中奖概率为$\frac{3}{8}$;
对于B,游戏盘的中奖概率为$\frac{2}{6}$=$\frac{1}{3}$;
对于C,游戏盘的中奖概率为1-$\frac{π{r}^{2}}{4{r}^{2}}$=1-$\frac{π}{4}$;
对于D,游戏盘的中奖概率为$\frac{\frac{1}{2}•2r•r}{π{r}^{2}}$=$\frac{1}{π}$;
其中A游戏盘的中奖概率最大.
故选:A.
点评 本题主要考查几何概型中的面积类型,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
20.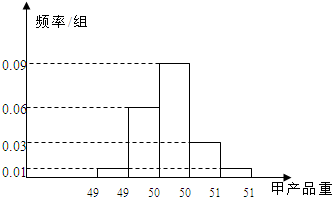 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
已知产品的重量合格标准为:重量值落在(495,510]内的产品为合格品;否则为不合格品.
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:| 乙流水线 产品重量(单位:克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
10.用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”的第二步是( )
| A. | 证明假设n=k(k≥1且k∈N)时正确,可推出n=k+1正确 | |
| B. | 证明假设n=2k+1(k≥1且k∈N)时正确,可推出n=2k+3正确 | |
| C. | 证明假设n=2k-1(k≥1且k∈N)时正确,可推出n=2k+1正确 | |
| D. | 证明假设n≤k(k≥1且k∈N)时正确,可推出n=k+2时正确 |
14.同时掷两个骰子,则向上的点数和为8的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{7}{36}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{4}$ |
 过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点
过曲线C:y=ex上一点P0(0,1)作曲线C的切线l0交x轴于点Q1(x1,0),又过Q1作x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点