题目内容

10．复数（1+i）z=3+i，则$\overline{z}$=（　　）
A．1+2iB．1-2iC．2-iD．2+i

分析 把已知等式变形，再由复数代数形式的乘除运算化简复数z得答案．

解答 解：由（1+i）z=3+i，
得$z=\frac{3+i}{1+i}=\frac{（3+i）（1-i）}{（1+i）（1-i）}=\frac{4-2i}{2}=2-i$，
则$\overline{z}$=2+i．
故选：D．

点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
20．函数y=|x|的图象是（　　）
A．B．C．D．
1．函数f（x）=|x-a|，a＜0
（Ⅰ）若a=-2求不等式f（x）+f（2x）＞2的解集
（Ⅱ）若不等式f（x）+f（2x）＜$\frac{1}{2}$的解集非空，求a的取值范围．
18．函数f（x）=x3-3x（-1＜x＜1）（　　）
A．有最大值，但无最小值B．有最大值，也有最小值
C．无最大值，也无最小值D．无最大值，但有最小值
5．已知tan=$\frac{1}{2}$，$\frac{2sinx+3cosx}{cosx-sinx}$的值为（　　）
A．-7B．8C．-8D．7
15．函数f（x）=2x-sinx在（-∞，+∞）上（　　）
A．是增函数B．是减函数
C．在（0，+∞）上增，在（-∞，0）上减D．在（0，+∞）上减，在（-∞，0）上增
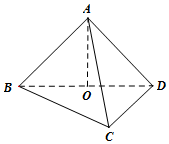2．（文科）设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O，
AC=BC=1，CD=$\sqrt{2}$，
求（1）AC与平面BCD所成角的大小；
（2）异面直线AB和CD的大小．
19．已知函数f（x）=2cos2x+2$\sqrt{3}$sinxcosx-1（x∈R）．
（1）把f（x）化简成f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的形式
（2）求函数f（x）的单调增区间．
20．求下列定积分：
（1）$\int_1^4{\sqrt{x}}（1-\sqrt{x}）dx$；
（2）$\int_1^2{\;}（{2^x}+\frac{1}{x}）dx$
（3）$\int_0^{\frac{Π}{3}}{\;}（sinx-sin2x）dx$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网