题目内容
若二次函数f(x)=ax2+bx+c(a≠0)的图象和直线y=x无交点,现有下列结论:
①方程f[f(x)]=x一定没有实数根;
②若a>0,则不等式f[f(x)]>x对一切实数x都成立;
③若a<0,则必存在实数x0,使f[f(x0)]>x0;
④函数g(x)=ax2-bx+c(a≠0)的图象与直线y=-x一定没有交点,
其中正确的结论是 (写出所有正确结论的编号).
①方程f[f(x)]=x一定没有实数根;
②若a>0,则不等式f[f(x)]>x对一切实数x都成立;
③若a<0,则必存在实数x0,使f[f(x0)]>x0;
④函数g(x)=ax2-bx+c(a≠0)的图象与直线y=-x一定没有交点,
其中正确的结论是
考点:二次函数的性质
专题:函数的性质及应用
分析:由函数f(x)的图象与直线y=x没有交点,所以f(x)>x(a>0)或f(x)<x(a<0)恒成立.进而逐一由此判断①~⑤的真假即可得到答案.
解答:
解:∵函数f(x)的图象与直线y=x没有交点,所以f(x)>x(a>0)或f(x)<x(a<0)恒成立.
因为f[f(x)]>f(x)>x或f[f(x)]<f(x)<x恒成立,所以f[f(x)]=x没有实数根;
故①正确;
若a>0,由题意知,二次函数的图象必在直线y=x的图象上方,则不等式f[f(x)]>f(x)>x对一切实数x都成立;
故②正确;
若a<0,由题意知,二次函数的图象必在直线y=x的图象下方,则不等式f[f(x)]<x对一切实数x都成立,所以不存在x0,使f[f(x0)]>x0;
故③错误;
函数g(x)=f(-x),与f(x)的图象关于y轴对称,所以g(x)和直线y=-x也一定没有交点.
故④正确;
故正确的结论有:①②④
故答案为:①②④
因为f[f(x)]>f(x)>x或f[f(x)]<f(x)<x恒成立,所以f[f(x)]=x没有实数根;
故①正确;
若a>0,由题意知,二次函数的图象必在直线y=x的图象上方,则不等式f[f(x)]>f(x)>x对一切实数x都成立;
故②正确;
若a<0,由题意知,二次函数的图象必在直线y=x的图象下方,则不等式f[f(x)]<x对一切实数x都成立,所以不存在x0,使f[f(x0)]>x0;
故③错误;
函数g(x)=f(-x),与f(x)的图象关于y轴对称,所以g(x)和直线y=-x也一定没有交点.
故④正确;
故正确的结论有:①②④
故答案为:①②④
点评:本题考查的知识点是命题的真假判断与应用,其中根据已知得到f(x)>x(a>0)或f(x)<x(a<0)恒成立是解答本题的关键.

练习册系列答案
相关题目
下列命题中真命题是( )
| A、命题“存在x∈R,x2-x-2≥0”的否定是:“不存在x∈R,x2-x-2<0” | ||||||||||
B、线性回归直线
| ||||||||||
C、存在x∈(0,
| ||||||||||
D、函数f(x)=x
|
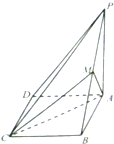 如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
如图,在四棱锥P-ABCD中,ABCD为平行四边形,BC⊥平面PAB,AB=BC=
