题目内容
莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞,某学校文学社从男女生中各抽取100名学生调查对莫言作品的了解程度,对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”.调查结果如下表:
参考数据:K2=
(1)求m,n的值;
(2)在犯错误的概率下不超过多少的前提下认为“对莫言作品非常了解与性别有关”?
| 男生 | 女生 | 合计 | |
| 非常了解 | 80 | m | 140 |
| 一般了解 | n | 40 | 60 |
| 合计 | 100 | 100 | 200 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 2.15 | 0.10 | 0.02 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)在犯错误的概率下不超过多少的前提下认为“对莫言作品非常了解与性别有关”?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据列联表,可求m,n的值;
(2)利用独立性检验的知识进行判断.
(2)利用独立性检验的知识进行判断.
解答:
解:(1)m=100-40=60,n=60-40=20;
(2)根据列联表数据得,K2=
≈9.524>7.879,
所以犯错误的概率下不超过0.005的前提下认为“对莫言作品非常了解与性别有关”.
(2)根据列联表数据得,K2=
| 200×(80×40-60×20)2 |
| 140×60×100×100 |
所以犯错误的概率下不超过0.005的前提下认为“对莫言作品非常了解与性别有关”.
点评:本题主要考查独立性检验的应用,利用列联表计算出K2,是解决本题的关键.这类题目主要是通过计算数据来进行判断的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a∈R,则“a≥0”是“函数f(x)=x2+|x-a|在(-∞,0]上是减函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
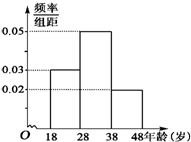 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: 在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=
在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=