题目内容
一次考试中,要求考生从试卷上的10个题目中任选3道题解答,其中6道甲类题,4道乙类题.
(Ⅰ)求考生所选题目都是甲类题的概率;
(Ⅱ)已知一考生所选的三道题目中有2道甲类题,1道乙类题,设该考生答对每道甲类题的概率都是
,答对每道乙类题的概率都是
,且各题答对与否相互独立,用X表示该考生答对题的个数,求X的分布列与数学期望.
(Ⅰ)求考生所选题目都是甲类题的概率;
(Ⅱ)已知一考生所选的三道题目中有2道甲类题,1道乙类题,设该考生答对每道甲类题的概率都是
| 3 |
| 5 |
| 4 |
| 5 |
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用古典概型概率计算公式能求出考生所选题目都是甲类题的概率.
(2)X所有的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
(2)X所有的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答:
解:(1)设事件A=“考生所选题目都是甲类题”,
则P(A)=
=
.
(2)X所有的可能取值为0,1,2,3,
P(X=0)=
(
)0(
)2•
=
,
P(X=1)=
(
)(
)•
+
(
)0(
)2•
=
,
P(X=2)=
(
)2(
)0•
+
(
)(
)•
=
,
P(X=3)=
(
)2(
)0•
=
,
∴X的分布列为:
∴EX=0×
+1×
+2×
+3×
=2.
则P(A)=
| ||
|
| 1 |
| 6 |
(2)X所有的可能取值为0,1,2,3,
P(X=0)=
| C | 0 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 4 |
| 125 |
P(X=1)=
| C | 1 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| C | 0 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 28 |
| 125 |
P(X=2)=
| C | 2 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| C | 1 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 57 |
| 125 |
P(X=3)=
| C | 2 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 36 |
| 125 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 24 |
| 125 |
| 28 |
| 125 |
| 57 |
| 125 |
| 36 |
| 125 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设随机变量X~B(2,P),随机变量Y~B(3,P),若P(X≥1)=
,则P(Y≥1)等于( )
| 5 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在等比数列{an}中,若a1a2a3=-8,则a2等于( )
A、-
| ||
| B、-2 | ||
C、±
| ||
| D、±2 |
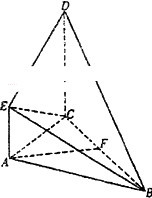 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.