题目内容
函数f(x)=
和函数g(x)=asin
x-a+1 (a>0),若存在x1,x2∈[0,1]使得f(x1)=g(x2)成立,则实数a的取值范围是 .
|
| π |
| 6 |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据给出的函数f(x)的解析式求出其值域,然后求出函数g(x)在x∈[0,1]上的值域,由存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数g(x)的最值中至少一个在范围内,最后列式求解a的范围.
解答:
解:当
<x≤1,f(x)=
,f′(x)=
=
>0,
所以函数f(x)在
<x≤1上为增函数,所以f(x)∈(
,
],
当x∈[0,
]时,函数f(x)=-(x-
)2+
为增函数,f(x)∈[-
,
],
所以在[0,1]上f(x)∈[-
,
],
函数g(x)=asin
x-a+1 (a>0),
当x∈[0,1]时,sin
x∈[0,
],
所以g(x)∈[1-a,1-
],
若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数函数g(x)的最大值与最小值中至少一个在[-
,
]内,
所以-
≤1-a≤
,-
≤1-
≤
,
即
≤a≤
或1≤a≤
即
≤a≤
,
所以实数a的取值范围是
≤a≤
,
故答案为:[
,
]
| 1 |
| 2 |
| x3 |
| x+1 |
| 3x2(x+1)-x3 |
| (x+1)2 |
| 2x3+3x2 |
| (x+1)2 |
所以函数f(x)在
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 2 |
当x∈[0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 12 |
所以在[0,1]上f(x)∈[-
| 1 |
| 6 |
| 1 |
| 2 |
函数g(x)=asin
| π |
| 6 |
当x∈[0,1]时,sin
| π |
| 6 |
| 1 |
| 2 |
所以g(x)∈[1-a,1-
| a |
| 2 |
若存在x1、x2∈[0,1],使得f(x1)=g(x2)成立,说明函数函数g(x)的最大值与最小值中至少一个在[-
| 1 |
| 6 |
| 1 |
| 2 |
所以-
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| a |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 7 |
| 6 |
| 7 |
| 3 |
即
| 1 |
| 2 |
| 7 |
| 3 |
所以实数a的取值范围是
| 1 |
| 2 |
| 7 |
| 3 |
故答案为:[
| 1 |
| 2 |
| 7 |
| 3 |
点评:本题主要考查函数的零点及函数的零点存在性定理,考查了数学转化思想,本题把函数的零点的研究转化为元素与集合之间的关系问题.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB中点.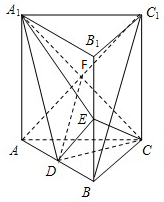 如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点,
如图,在三棱柱ABC---A1B1C1中,D、E分别是AB、BB1的中点, 如图两个等边△ABC,△ACD所在的平面互相垂直,EB⊥平面ABC,且AC=2,
如图两个等边△ABC,△ACD所在的平面互相垂直,EB⊥平面ABC,且AC=2,