题目内容
已知a∈R,则“a≥0”是“函数f(x)=x2+|x-a|在(-∞,0]上是减函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:化函数为分段函数,分别由二次函数的单调性可得a的范围,可得答案.
解答:
解:∵f(x)=x2+|x-a|=
,
由二次函数可知y=x2+x-a在(-∞,-
)单调递减,(-
,+∞)单调递增,
∴必有a≥0,
同理可得y=x2-x+a在(-∞,
)单调递减,(
,+∞)单调递增,
∴亦必有a≥0,
综合可得a≥0,
故“a≥0”是“函数f(x)=x2+|x-a|在(-∞,0]上是减函数”的充要条件
故选:C.
|
由二次函数可知y=x2+x-a在(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
∴必有a≥0,
同理可得y=x2-x+a在(-∞,
| 1 |
| 2 |
| 1 |
| 2 |
∴亦必有a≥0,
综合可得a≥0,
故“a≥0”是“函数f(x)=x2+|x-a|在(-∞,0]上是减函数”的充要条件
故选:C.
点评:本题考查充要条件的判定,涉及二次函数的单调性,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{cn}的通项是cn=
,则数列{cn}中的正整数项有( )项.
| 4n+31 |
| 2n-1 |
| A、1 | B、2 | C、3 | D、4 |
设随机变量X~B(2,P),随机变量Y~B(3,P),若P(X≥1)=
,则P(Y≥1)等于( )
| 5 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
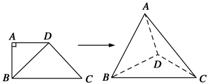 如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )
如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |
集合A={0,1,2,3,4},B={x|x<2},则A∩B=( )
| A、∅ |
| B、{0,1} |
| C、{0,1,2} |
| D、{x|x<2} |
在等比数列{an}中,若a1a2a3=-8,则a2等于( )
A、-
| ||
| B、-2 | ||
C、±
| ||
| D、±2 |