题目内容
在五边形ABCDE中(图一),BD是AC的垂直平分线,O为垂足.ED∥AC,AE∥BD,AB⊥BC.沿对角线AC将四边形ACDE折起,使平面ACDE⊥平面ABC(图二).
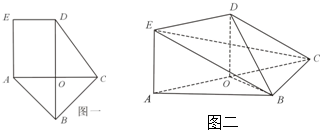
(1)求证:平面EBC⊥平面EAB;
(2)若OD=OB=1,求点A到平面DBC的距离.

(1)求证:平面EBC⊥平面EAB;
(2)若OD=OB=1,求点A到平面DBC的距离.
考点:平面与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由已知条件推导出OD⊥平面ABC,从而得AE⊥BC,进而得到BC⊥平面EAB,由此能证明平面EBC⊥平面EAB.
(2)连AD,设点A到平面DBC的距离为d,由VA-DBC=VD-ABC,利用等积法能求出点A到平面DBC的距离.
(2)连AD,设点A到平面DBC的距离为d,由VA-DBC=VD-ABC,利用等积法能求出点A到平面DBC的距离.
解答:
(1)证明:∵平面ACDE⊥平面ABC,OD⊥AC,
∴OD⊥平面ABC,…(2分)
∵AE∥OD,∴AE⊥平面ABC,∴AE⊥BC,
又∵AB⊥BC,∴BC⊥平面EAB,
∵BC∥平面EBC,
∴平面EBC⊥平面EAB.…(6分)
(2)解:∵OD=OB=1,
∴BC=DB=DC=
,
S△DBC=
×(
)2=
…(8分)
连AD,设点A到平面DBC的距离为d,
∵VA-DBC=VD-ABC
∴
•S△DBC•d=
•
•AC•OB•OD,
整理,得
d=1,解得d=
.…(12分)
∴OD⊥平面ABC,…(2分)
∵AE∥OD,∴AE⊥平面ABC,∴AE⊥BC,
又∵AB⊥BC,∴BC⊥平面EAB,
∵BC∥平面EBC,
∴平面EBC⊥平面EAB.…(6分)

(2)解:∵OD=OB=1,
∴BC=DB=DC=
| 2 |
S△DBC=
| ||
| 4 |
| 2 |
| ||
| 2 |
连AD,设点A到平面DBC的距离为d,
∵VA-DBC=VD-ABC
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
整理,得
| ||
| 2 |
2
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
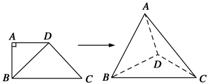 如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )
如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )| A、平面ABD⊥平面ABC |
| B、平面ADC⊥平面BDC |
| C、平面ABC⊥平面BDC |
| D、平面ADC⊥平面ABC |
 如图,四棱锥P-ABCD中,侧面PAD为等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形,AB∥CD,AB=2CD,BC⊥CD,∠DBC=30°,点E,F分别为AD,PB中点.